题目内容
已知定义域为R的偶函数y=f(x)在[0,+∞)上单调递增,其图象均在x轴上方,对任意m,n∈[0,+∞),都有f(m•n)=[f(m)]n,且f(2)=4.
(1)求f(0)、f(-1)的值;
(2)解关于x的不等式[f(
)]2≥2,其中k∈(-1,1).
(1)求f(0)、f(-1)的值;
(2)解关于x的不等式[f(
| kx+2 | ||
2
|
(1)由题意知对任意x∈R,f(x)>0,
又对任意m,n∈[0,+∞),都有f(mn)=[f(m)]n,
则令m=n=0则f(0)=[f(0)]0=1,…(2分)
令m=1,n=2,可得f(2)=f(1×2)=[f(1)]2=4,
∴f(1)=2,根据偶函数的性质可知f(-1)=2.…(6分)
(2)[f(
)]2≥2?f(
)≥f(±1)…(9分)
∵f(x)为偶函数,且在[0,+∞)上单调递增,∴|
|≥1,
即(k2-1)x2+4kx≥0…(11分)
当-1<k<0时,原不等式的解集为[
,0];
当k=0时,原不等式的解集为{0};
当0<k<1时,原不等式的解集为[0,
].…(14分)
又对任意m,n∈[0,+∞),都有f(mn)=[f(m)]n,
则令m=n=0则f(0)=[f(0)]0=1,…(2分)
令m=1,n=2,可得f(2)=f(1×2)=[f(1)]2=4,
∴f(1)=2,根据偶函数的性质可知f(-1)=2.…(6分)
(2)[f(
| kx+2 | ||
2
|
| kx+2 | ||
|
∵f(x)为偶函数,且在[0,+∞)上单调递增,∴|
| kx+2 | ||
|
即(k2-1)x2+4kx≥0…(11分)
当-1<k<0时,原不等式的解集为[
| 4k |
| 1-k2 |
当k=0时,原不等式的解集为{0};
当0<k<1时,原不等式的解集为[0,
| 4k |
| 1-k2 |

练习册系列答案
相关题目
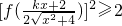 ,其中k∈(-1,1).
,其中k∈(-1,1).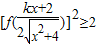 ,其中k∈(-1,1).
,其中k∈(-1,1).