题目内容
8.已知函数f(x)=$\frac{alnx+b}{x}$(其中a≤2且a≠0),函数f(x)在点(1,f(1))处的切线过点(3,0).(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)与函数g(x)=a+2-x-$\frac{2}{x}$的图象在(0,2]有且只有一个交点,求实数a的取值范围.
分析 (1)利用导数的几何意义可得切线方程,对a分类讨论、利用导数研究函数的单调性即可;
(2)等价方程$\frac{alnx+2a}{x}=a+2-x-\frac{2}{x}$在(0,2]只有一个根,即x2-(a+2)x+alnx+2a+2=0在(0,2]只有一个根,令h(x)=x2-(a+2)x+alnx+2a+2,等价函数h(x)在(0,2]与x轴只有唯一的交点.由$h'(x)=\frac{(2x-a)(x-1)}{x}$,对a分类讨论、结合图象即可得出.
解答 解:(1)$f(x)=\frac{alnx+b}{x}$,
∴f(1)=b,${f}^{′}(x)=\frac{a-b-alnx}{{x}^{2}}{|}_{x=1}$=a-b,
∴y-b=(a-b)(x-1),
∵切线过点(3,0),
∴b=2a,
∴$f'(x)=\frac{a-b-alnx}{x^2}=-\frac{a(lnx+1)}{x^2}$,
①当a∈(0,2]时,$x∈(0,\frac{1}{e})$单调递增,$x∈(\frac{1}{e},+∞)$单调递减,
②当a∈(-∞,0)时,$x∈(0,\frac{1}{e})$单调递减,$x∈(\frac{1}{e},+∞)$单调递增.
(2)等价方程$\frac{alnx+2a}{x}=a+2-x-\frac{2}{x}$在(0,2]只有一个根,
即x2-(a+2)x+alnx+2a+2=0在(0,2]只有一个根,
令h(x)=x2-(a+2)x+alnx+2a+2,等价函数h(x)在(0,2]与x轴只有唯一的交点,
∴$h'(x)=\frac{(2x-a)(x-1)}{x}$
①当a<0时,h(x)在x∈(0,1)递减,x∈(1,2]的递增,
当x→0时,h(x)→+∞,要函数h(x)在(0,2]与x轴只有唯一的交点,
∴h(1)=0或h(2)<0,
∴a=-1或$a<-\frac{2}{ln2}$.
②当a∈(0,2)时,h(x)在$x∈(0,\frac{a}{2})$递增,$x∈(\frac{a}{2},1)$的递减,x∈(1,2]递增,
∵$h(\frac{a}{2})>h(1)=a+1>0$,当x→0时,h(x)→-∞,
∵h(e-4)=e-8-e-4-2<0,
∴h(x)在$x∈(0,\frac{a}{2})$与x轴只有唯一的交点,
③当a=2,h(x)在x∈(0,2]的递增,
∵h(e-4)=e-8-e-4-2<0,或f(2)=2+ln2>0,
∴h(x)在x∈(0,2]与x轴只有唯一的交点,
故a的取值范围是a=-1或$a<-\frac{2}{ln2}$或0<a≤2.
点评 本题考查了利用导数研究函数的单调性极值与最值、导数的几何意义,考查了恒成立问题的等价转化方法,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{{\sqrt{2}}}{2}}$) | C. | $({\frac{{\sqrt{2}}}{2},1})$ | D. | $({\frac{1}{2},1})$ |
| A. | $\frac{1}{4}$ | B. | 1 | C. | $\frac{5}{4}$ | D. | 2 |
| A. | -2i | B. | 2i | C. | -4i | D. | 4i |
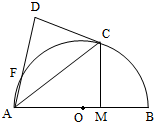 如图,AB是圆O的直径,C、F为圆O上的点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M.若圆O的半径为1,∠BAC=30°,则DF•AM=$\frac{3}{4}$.
如图,AB是圆O的直径,C、F为圆O上的点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M.若圆O的半径为1,∠BAC=30°,则DF•AM=$\frac{3}{4}$.