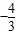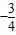题目内容
已知
，且α
，那么tanα的值为（ ）A．
B．
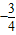
C．
D．
【答案】分析：由sinα的值及α的范围，利用同角三角函数间的基本关系求出cosα的值，进而再由同角三角函数间的基本关系弦化切后，即可求出tanα的值．
解答：解：∵
，且α
，
∴cosα=-
=-
，
则tanα=
=-
．
故选A
点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键，同时注意角度的范围．
解答：解：∵
，且α，∴cosα=-
=-，则tanα=
=-．故选A
点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键，同时注意角度的范围．
练习册系列答案
相关题目
，且
，那么
的值等于____________. 
个单位，再将横坐标伸长到原来的2倍，纵坐标不变，得到函数g（x）的图象，求g（x）的解析式；
，且
，求tan（x1+x2）的值．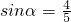
，且α
，那么tanα的值为
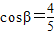，且
，那么tanβ的值等于（ ）
