题目内容
已知x,y满足
,不等式x2+9y2≥axy恒成立,则a的取值范围为
|
a≤
| 15 |
| 2 |
a≤
.| 15 |
| 2 |
分析:
等价于
或
,作出可行域,得到可行域为△ABC,顶点坐标分别为A(3,2),B(2,3),C(1,2),由此能求出不等式x2+9y2≥axy恒成立a的取值范围.
|
|
|
解答: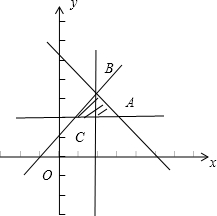 解:
解:
等价于
或
,
作出可行域,得到可行域为△ABC,顶点坐标分别为A(3,2),B(2,3),C(1,2),
把A(3,2)代入x2+9y2≥axy,得a≤
;
把B(2,3)代入x2+9y2≥axy,得a≤
;
把C(1,2)代入x2+9y2≥axy,得a≤
.
∴a的取值范围为:a≤
.
故答案为:a≤
.
 解:
解:
|
|
|
作出可行域,得到可行域为△ABC,顶点坐标分别为A(3,2),B(2,3),C(1,2),
把A(3,2)代入x2+9y2≥axy,得a≤
| 15 |
| 2 |
把B(2,3)代入x2+9y2≥axy,得a≤
| 85 |
| 6 |
把C(1,2)代入x2+9y2≥axy,得a≤
| 37 |
| 2 |
∴a的取值范围为:a≤
| 15 |
| 2 |
故答案为:a≤
| 15 |
| 2 |
点评:本题考查函数恒成立问题,解题时要认真审题,注意线性规划的灵活运用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目