题目内容
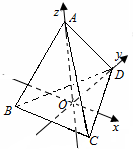如图，三棱锥A-BCD是正三棱锥，O为底面BCD的中心，以O为坐标原点，分别以OD、OA为y、z轴建立如图所示的空间直角坐标系O-xyz，若|| OA |
| BC |
分析：利用等边三角形的重心的性质可得点C的坐标，再利用中点坐标公式即可得出线段AC的中点坐标．
解答：解：∵|
|=|
|=12，∴A（0，0，12），xC=6．
由等边△BCD，点O是重心，可得yC=-
×6
=-2
，
∴C(6，-2
，0)．
设线段AC的中点坐标E（x，y，z），则
，解得x=3，y=-
，z=12．
∴E(3，-
，6)．
故答案为：(3，-
，6)．
| OA |
| BC |
由等边△BCD，点O是重心，可得yC=-
| 1 |
| 3 |
| 3 |
| 3 |
∴C(6，-2
| 3 |
设线段AC的中点坐标E（x，y，z），则
|
| 3 |
∴E(3，-
| 3 |
故答案为：(3，-
| 3 |
点评：本题考查了等边三角形的重心的性质、中点坐标公式，属于基础题．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
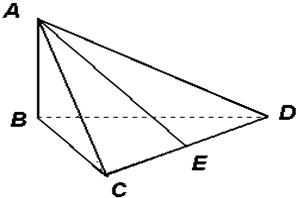如图，三棱锥A-BCD中，AB⊥底面BCD，BC⊥CD，且AB=BC=1，CD=2，点E为CD的中点，则AE的长为（ ）
如图，三棱锥A-BCD，BC=3，BD=4，CD=5，AD⊥BC，E，F分别是棱AB，CD的中点，连接CE，G为CE上一点．
如图，三棱锥A-BCD的底面是等腰直角三角形，AB⊥平面BCD，AB=BC=BD=2，E是棱CD上的任意一点，F、G分别是AC、BC的中点，则在下面的命题中：①平面ABE⊥平面BCD；②平面EFG∥平面ABD；③四面体FECG的体积最大值是
（2009•滨州一模）如图，三棱锥A-BCD中，AD、BC、CD两两互相垂直，且AB=13，BC=3，CD=4，M、N分别为AB、AC的中点．