题目内容
(本题满分10分)已知函数  .
.
(Ⅰ) 若  ,求函数
,求函数  的单调区间;
的单调区间;
(Ⅱ)若函数  的图像在点
的图像在点  处的切线的斜率是1,问:
处的切线的斜率是1,问:
 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的  ,函数
,函数  在区间
在区间  上总存在极值?
上总存在极值?
【答案】
22解:(1)由 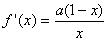 知:
知:
当 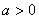 时,函数
时,函数  的单调增区间是
的单调增区间是 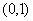 ,单调减区间是
,单调减区间是 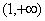 ;
;
(2)由 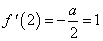
 ,
,
∴  ,
,  .
.
故 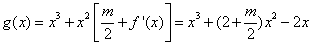 ,
,
∴  ,
,
∵ 函数 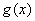 在区间
在区间 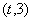 上总存在极值,∴ 函数
上总存在极值,∴ 函数
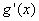 在区间
在区间 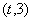 上总存在零点,
上总存在零点,
又∵函数 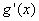 是开口向上的二次函数,且
是开口向上的二次函数,且 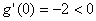
∴ 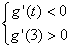
由 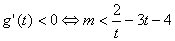 ,令
,令 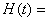
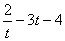 ,则
,则 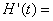
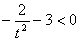 ,
,
所以  在
在 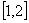 上单调递减,所以
上单调递减,所以 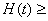
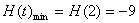 ;
;
由 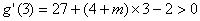 ,解得
,解得  ;
;
综上得 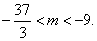
所以当 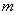 在
在 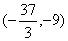 内取值时,对于任意的
内取值时,对于任意的 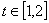 ,函数
,函数 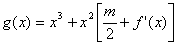 在区间
在区间 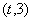 上总存在极值.
上总存在极值.
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.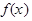 的单调区间;
的单调区间; 且
且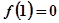 .
. 是偶函数,求函数
是偶函数,求函数 上的最大值和最小值;
上的最大值和最小值; 的取值范围.
的取值范围. ∩
∩ =m,a∥
=m,a∥