题目内容
已知向量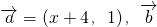 =(x2,2)则x=4是
=(x2,2)则x=4是 的
的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
A
分析:由于 ,则2(x+4)=x2,解得x=-2或x=4,结合集合关系,得到x=4是
,则2(x+4)=x2,解得x=-2或x=4,结合集合关系,得到x=4是 的充分不必要条件.
的充分不必要条件.
解答:由于向量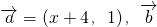 =(x2,2),
=(x2,2),
则 等价于2(x+4)=x2 ,
等价于2(x+4)=x2 ,
即x2-2x-8=0,解得x=-2或x=4,
由判断充要条件的方法,我们可知若A B,则命题“x∈A”是命题“x∈B”的充分不必要条件,
B,则命题“x∈A”是命题“x∈B”的充分不必要条件,
则x=4是 的充分不必要条件,故答案选A.
的充分不必要条件,故答案选A.
点评:本题考查充分条件、必要条件与充要条件判断.要判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.由判断充要条件的方法,我们可知命题“x∈A”是命题“x∈B”的充分不必要条件,则A B.
B.
分析:由于
 ,则2(x+4)=x2,解得x=-2或x=4,结合集合关系,得到x=4是
,则2(x+4)=x2,解得x=-2或x=4,结合集合关系,得到x=4是 的充分不必要条件.
的充分不必要条件.解答:由于向量
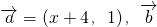 =(x2,2),
=(x2,2),则
 等价于2(x+4)=x2 ,
等价于2(x+4)=x2 ,即x2-2x-8=0,解得x=-2或x=4,
由判断充要条件的方法,我们可知若A
 B,则命题“x∈A”是命题“x∈B”的充分不必要条件,
B,则命题“x∈A”是命题“x∈B”的充分不必要条件,则x=4是
 的充分不必要条件,故答案选A.
的充分不必要条件,故答案选A.点评:本题考查充分条件、必要条件与充要条件判断.要判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.由判断充要条件的方法,我们可知命题“x∈A”是命题“x∈B”的充分不必要条件,则A
 B.
B. 
练习册系列答案
相关题目