题目内容
若函数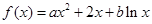 在
在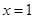 和
和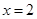 处取得极值,
处取得极值,
(1)求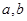 的值;
的值;
(2)求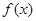 在
在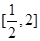 上的最大值和最小值.
上的最大值和最小值.
【答案】
(1)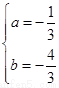 (2)最大值为
(2)最大值为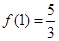 ,最小值为
,最小值为
【解析】(1)先求出导函数,然后利用极值的性质求出参数a和b;(2)先用导数法求出函数在给定区间内的单调区间,然后利用单调性求出函数的最值
1)由题意 , 由
, 由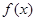 在
在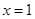 和
和 处取得极值得
处取得极值得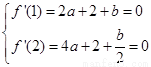 解得
解得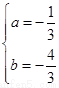 ……7分
……7分
(2)由(1)知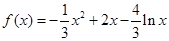 ,故
,故
 由
由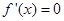 得
得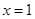 或
或
在 上当
上当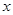 变化时,
变化时,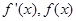 变化情况列表得
变化情况列表得
|
|
|
1 |
|
|
|
— |
0 |
+ |
|
|
单调递减 |
极大值 |
单调递增 |
所以,当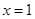 时,
时,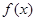 取得极大值
取得极大值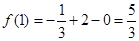
又 ,
,
所以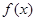 在
在 上的最大值为
上的最大值为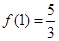 ,最小值为
,最小值为

练习册系列答案
相关题目


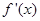
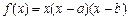 ,点
,点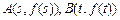 .
.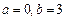 ,函数
,函数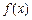 在
在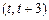 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求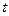 的取值范围;
的取值范围;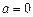 时,
时,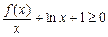 对任意的
对任意的 恒成立,求
恒成立,求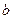 的取值范围;
的取值范围;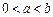 ,函数
,函数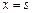 和
和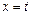 处取得极值,且
处取得极值,且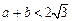 ,
,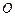 是坐标原点,证明:直线
是坐标原点,证明:直线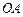 与直线
与直线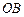 不可能垂直.
不可能垂直.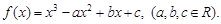 .
.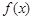 在
在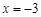 和
和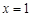 处取得极值,试求
处取得极值,试求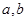 的值;
的值;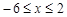 时,
时,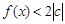 恒成立,求c的取值范围.
恒成立,求c的取值范围.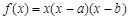 ,点
,点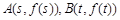 .
. ,函数
,函数 在
在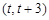 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求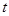 的取值范围;
的取值范围;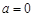 时,
时, 对任意的
对任意的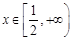 恒成立,求
恒成立,求 的取值范围;
的取值范围; ,函数
,函数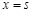 和
和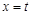 处取得极值,且
处取得极值,且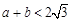 ,
, 是坐标原点,证明:直线
是坐标原点,证明:直线 与直线
与直线 不可能垂直.
不可能垂直.