题目内容
(本题满分12分)已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.

(Ⅰ)证明:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)![]() 为
为![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]()
![]() ∥平面
∥平面![]() ,若存在,求出
,若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
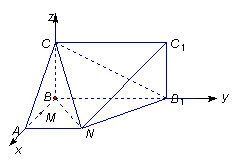 (Ⅰ)法一:证明∵该几何体的正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形,
(Ⅰ)法一:证明∵该几何体的正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形,
∴BA,BC,BB1两两垂直.以BA, BB1,BC分别为
x,y,z轴建立空间直角坐标系,
则B(0,0,0),N(4,4,0),B1(0,8,0),C1(0,8,4),C(0,0,4)
∵![]() (4,4,0)(-4,4,0)
(4,4,0)(-4,4,0)![]()
![]() (4,4,0)(0,0,4)=0 ……3分
(4,4,0)(0,0,4)=0 ……3分
∴BN⊥NB1, BN⊥B1C1.又NB1与B1C1相交于B1,
∴BN⊥平面C1B1N. …………4分
法二:∵该几何体的正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形,
∴BA,BC,BB1两两垂直.∴BC⊥平面ANB1B
∵BC∥B1C1∴B1C1⊥平面ANB1B,∴BN⊥B1C1 ………2分
取BB1中点D,连结ND.
则ANDB是正方形,NDB1是等腰直角三角形
![]() 又
又![]()
![]()
![]() ,
,![]() …………4分
…………4分
(Ⅱ)法一:∵BN⊥平面C1B1N![]()
![]() 是平面C1B1N的一个法向量
是平面C1B1N的一个法向量![]() =(4,4,0),
=(4,4,0),
设![]() 为平面NCB1的一个法向量,则
为平面NCB1的一个法向量,则
 ,
,![]() ,
,![]()
![]()
则
由图可知,所求二面角为锐角,
所以,所求二面角C-NB1-C1的余弦值为![]() . …………9分
. …………9分
法二:只要求二面角![]() 的正弦值,由(Ⅰ)易证
的正弦值,由(Ⅰ)易证![]() 为二面角
为二面角![]() 的平面角,
的平面角,![]() ,
,![]() ,
,
![]() ,故所求二面角C-NB1-C1的余弦值为
,故所求二面角C-NB1-C1的余弦值为![]()
(Ⅲ)∵![]() .设
.设![]() (
(![]() )为
)为![]() 上一点,则
上一点,则![]() ,
,
![]() ∥平面
∥平面![]() ,
, ![]()
∴![]()
![]() ,
, ![]()
∴在CB上存在一点P(0,0,1), ![]() ∥平面
∥平面![]() 且
且![]() ………12分
………12分

 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点. ,且
,且 ,
, ,求
,求 作以
作以 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围