题目内容
已知l1和l2是平面内互相垂直的两条直线,它们的交点为A,动点B、C分别在l1和l2上,且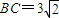 ,过A、B、C三点的动圆所形成的区域的面积为 .
,过A、B、C三点的动圆所形成的区域的面积为 .
【答案】分析:由题意可知当A与B或C重合时,所成的圆最大,它包括了所有的圆,所以求出半径为3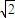 时圆的面积即为动圆所形成的区域的面积.
时圆的面积即为动圆所形成的区域的面积.
解答:解:当A与B或C重合时,此时圆的面积最大,此时圆的半径r=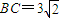 ,
,
所以此时圆的面积S=πr2=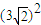 π=18π,
π=18π,
则过A、B、C三点的动圆所形成的区域的面积为18π
故答案为18π
点评:学生作此题时应注意:过A、B、C三点的动圆所形成的区域面积,不是过A、B、C三点的圆的面积.而是将所有圆的面积(只能算不重合的部分)即半径为BC最大圆的面积.此题是一道易错题.
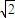 时圆的面积即为动圆所形成的区域的面积.
时圆的面积即为动圆所形成的区域的面积.解答:解:当A与B或C重合时,此时圆的面积最大,此时圆的半径r=
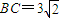 ,
,所以此时圆的面积S=πr2=
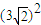 π=18π,
π=18π,则过A、B、C三点的动圆所形成的区域的面积为18π
故答案为18π
点评:学生作此题时应注意:过A、B、C三点的动圆所形成的区域面积,不是过A、B、C三点的圆的面积.而是将所有圆的面积(只能算不重合的部分)即半径为BC最大圆的面积.此题是一道易错题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 ,过A、B、C三点的动圆所形成的区域的面积为 .
,过A、B、C三点的动圆所形成的区域的面积为 .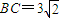 ,过A、B、C三点的动圆所形成的区域的面积为 .
,过A、B、C三点的动圆所形成的区域的面积为 .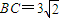 ,过A、B、C三点的动圆所形成的区域的面积为 .
,过A、B、C三点的动圆所形成的区域的面积为 .