题目内容
|AB|=|xA-xB|表示数轴上A,B两点的距离,它也可以看作满足一定条件的一种运算.这样,可以将满足下列三个条件的一个x与y间的运算p(x,y)叫做x,y之间的距离:条件一,非负性p(x,y)≥0,等号成立当且仅当x=y;条件二,交换律p(x,y)=p(y,x);条件三,三角不等式p(x,z)≤p(x,y)+p(y,z).试确定运算
 是否为一个距离?是,证明;不是,举出反例.
是否为一个距离?是,证明;不是,举出反例.
【答案】分析:要说明s(x,y)是否为距离,只要验证它是否满足三条即可.即满足条件一,非负性p(x,y)≥0,等号成立当且仅当x=y;条件二,交换律p(x,y)=p(y,x);条件三,三角不等式p(x,z)≤p(x,y)+p(y,z).
解答:解:①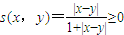 等号成立当且仅当|x-y|=0,即x=y,第一条满足
等号成立当且仅当|x-y|=0,即x=y,第一条满足
②s(x,y)=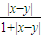 =
=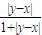 =s(y,x),第二条也满足
=s(y,x),第二条也满足
③s(x,z)=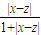
∵函数f(x)=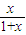 =1-
=1-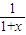 (或
(或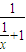 )在(0,+∞)上单调增,且|x-z|≤|x-y|+|y-z|
)在(0,+∞)上单调增,且|x-z|≤|x-y|+|y-z|
∴s(x,z)≤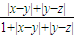 =
=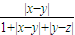 +
+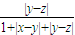
≤ +
+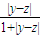 =s(x,y)+s(y,z),第三条也满足.
=s(x,y)+s(y,z),第三条也满足.
总之,s(x,y)是距离.
点评:本小题主要考查函数单调性的应用、综合法与分析法、绝对值不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想,属于基础题.
解答:解:①
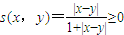 等号成立当且仅当|x-y|=0,即x=y,第一条满足
等号成立当且仅当|x-y|=0,即x=y,第一条满足②s(x,y)=
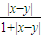 =
=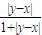 =s(y,x),第二条也满足
=s(y,x),第二条也满足③s(x,z)=
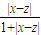
∵函数f(x)=
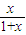 =1-
=1-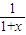 (或
(或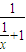 )在(0,+∞)上单调增,且|x-z|≤|x-y|+|y-z|
)在(0,+∞)上单调增,且|x-z|≤|x-y|+|y-z|∴s(x,z)≤
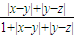 =
=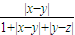 +
+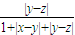
≤
 +
+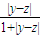 =s(x,y)+s(y,z),第三条也满足.
=s(x,y)+s(y,z),第三条也满足.总之,s(x,y)是距离.
点评:本小题主要考查函数单调性的应用、综合法与分析法、绝对值不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 抛物线y=b(
抛物线y=b( A∩B},已知两个开区间M=(a,b),N=(c,d),其中a.b.c.d满足a+b<c+d,ab=cd<0,则MN等于
A∩B},已知两个开区间M=(a,b),N=(c,d),其中a.b.c.d满足a+b<c+d,ab=cd<0,则MN等于