Question

18．在长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，AA₁=3，过A₁、C₁、B三点的平面截去长方体的一个角后，得到如下所示的几何体ABCD-A₁C₁D₁．
（1）若A₁C₁的中点为O₁，求异面直线BO₁与A₁D₁所成角的大小（结果用反三角函数值表示）；
（2）求点D到平面A₁BC₁的距离d．

Answer 1

分析 （1）建立空间直角坐标系．求出相关点的坐标，求出$\overrightarrow{B{O_1}}=（-1，-1，3），\overrightarrow{{A_1}{D_1}}=（-2，0，0）$．利用空间向量的连结求解异面直线BO₁与A₁D₁所成的角．
（2）求出平面ABD的法向量．通过空间向量的距离公式求解即可．

解答 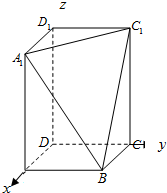（本题满分12分）本题共有2个小题，第1小题满分（6分），第2小题满分（6分）．（理科）
解：（1）按如图所示建立空间直角坐标系．由题知，可得点D（0，0，0）、B（2，2，0）、D₁（0，0，3）、A₁（2，0，3）、C₁（0，2，3）．　　　　　  
由O₁是A₁C₁中点，可得O₁（1，1，3）．
于是，$\overrightarrow{B{O_1}}=（-1，-1，3），\overrightarrow{{A_1}{D_1}}=（-2，0，0）$．
设异面直线BO₁与A₁D₁所成的角为θ，则
$cosθ=|{\frac{{\overrightarrow{B{O_1}}•\overrightarrow{{A_1}{D_1}}}}{{|\overrightarrow{B{O_1}}||\overrightarrow{{A_1}{D_1}}|}}}|=\frac{2}{{2\sqrt{11}}}=\frac{{\sqrt{11}}}{11}$．
因此，异面直线BO₁与A₁D₁所成的角为$arccos\frac{{\sqrt{11}}}{11}$．
（2）设$\overrightarrow n=（x，y，z）$是平面ABD的法向量．
∴$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{B{A_1}}=0\\ \overrightarrow n•\overrightarrow{B{C_1}}=0.\end{array}\right.$
又$\overrightarrow{B{A_1}}=（0，-2，3），\overrightarrow{B{C_1}}=（-2，0，3）$，
∴$\left\{\begin{array}{l}-2y+3z=0\\-2x+3z=0.\end{array}\right.$取z=2，可得$\left\{\begin{array}{l}x=3\\ y=3\\ z=2.\end{array}\right.$即平面BA₁C₁的一个法向量是$\overrightarrow n=（3，3，2）$．
∴$d=|{\frac{{\overrightarrow n•\overrightarrow{DB}}}{|\overrightarrow n|}}|$=$\frac{{6\sqrt{22}}}{11}$．

点评 本题考查空间点线面距离的求法，异面直线所成角的求法，考查空间想象能力以及计算能力．