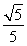Question

已知抛物线C:y²=2ax(a<0),过点(-1,0)作直线l交抛物线C于A、B两点.问是否存在以AB为直径且过抛物线C的焦点F的圆?

Answer 1

解析:设直线l的方程为y=k(x+1)(k≠0),代入抛物线方程得

k²x²+(2k²-2a)x+k²=0.①?

若存在以AB为直径且过焦点F的圆,则AF⊥BF.

设A、B的坐标分别为(x₁,y₁)、(x₂,y₂),?

则,

即k²(x₁+1)(x₂+1)+(x₁-)(x₂-)=0,②

由方程①有x₁+x₂=,x₁x₂=1.

代入②并整理得?

k²=.

∵k²>0,a<0,?

∴>0,a<0,?

即a²+12a+4>0且a<0.

解得a<-6-4或-6+4

又当k不存在时,即直线l⊥x轴,

此时直线l:x=-1.

可得A(-1,)、B(-1, ).

由k _AF·k _BF=-1得a=-6±4.

故当a≤-6-42或-6+42≤a<0时,存在满足题设的圆.

当-6-4＜a＜-6+42时,不存在这样的圆.