题目内容
已知函数![]() .
.
(Ⅰ)当m=时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)当m=1时,证明方程f(x)=g(x)有且仅有一个实数根;
(Ⅲ)若x∈(1,e]时,不等式f(x)-g(x)<2恒成立,求实数m的取值范围.
答案:
解析:
解析:
|
解:(Ⅰ) (Ⅱ) 又 (Ⅲ) 又 令 则 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
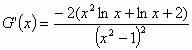 ,
, 满足:当x≥4时,
满足:当x≥4时, ;当x<4时
;当x<4时 ,则
,则 =______.
=______. .
. 的最大值;
的最大值;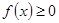 .
.


 时,讨论
时,讨论 的单调性:
的单调性:  ,当
,当 时,若对任意x1∈(0,2),存在
时,若对任意x1∈(0,2),存在 ∈
∈ ,使
,使 ,求实数b的取值范围。
,求实数b的取值范围。 ,
, 。
。 的单调区间;
的单调区间; 时,
时, 对任意正实数
对任意正实数 都成立;
都成立; ,使得
,使得 对任意的正实数
对任意的正实数 都成立,请直接写出满足这样条件的一个
都成立,请直接写出满足这样条件的一个