题目内容
下列结论正确的是
- A.
 在定义域内是单调递减函数
在定义域内是单调递减函数 - B.若f(x)在区间[0,2]上满足f(0)<f(2),则f(x)在[0,2]上是单调递增的
- C.若f(x)在区间[0,3]上单调递减,则f(x)在(1,2)上单调递减
- D.若f(x)在区间(1,2),[2,3]上分别单调递减,则f(x)在(1,3]上单调递减
C
分析:根据题意,依次分析选项,对于A、举出反例y= ,在其定义域中取特殊值-1与1,可以判断A错误,对于B、构造二次函数的图象,举出反例可得B错误,对于C、(1,2)是[0,3]的子集,由单调性的定义可得C正确,对于D、构造分段函数,举出反例可得D错误;即可得答案.
,在其定义域中取特殊值-1与1,可以判断A错误,对于B、构造二次函数的图象,举出反例可得B错误,对于C、(1,2)是[0,3]的子集,由单调性的定义可得C正确,对于D、构造分段函数,举出反例可得D错误;即可得答案.
解答: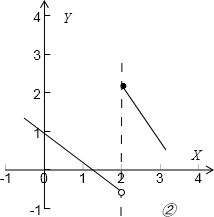
 解:根据题意,依次分析选项可得:
解:根据题意,依次分析选项可得:
对于A、y= 的定义域为x≠0,x取特殊值-1与1,有f(-1)=-4,f(4)=4,则f(-4)<f(4),故y=
的定义域为x≠0,x取特殊值-1与1,有f(-1)=-4,f(4)=4,则f(-4)<f(4),故y= 不是减函数,则A错误;
不是减函数,则A错误;
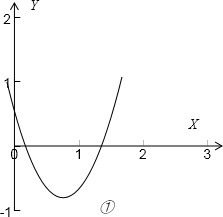
对于B、如图①,其中的函数,有f(0)<f(2),而f(x)在[0,2]上不是单调的,B错误;
对于C、(1,2)是[0,3]的子集,则若f(x)在区间[0,3]上单调递减,则f(x)在(1,2)上单调递减,则C正确;
对于D、如图②,f(x)在区间(1,2),[2,3]上分别单调递减,但f(x)在(1,3]上不是单调,D错误;
故选C.
点评:本题考查函数的单调性的判断,关键是理解函数单调性的定义,并能举出反例.
分析:根据题意,依次分析选项,对于A、举出反例y=
 ,在其定义域中取特殊值-1与1,可以判断A错误,对于B、构造二次函数的图象,举出反例可得B错误,对于C、(1,2)是[0,3]的子集,由单调性的定义可得C正确,对于D、构造分段函数,举出反例可得D错误;即可得答案.
,在其定义域中取特殊值-1与1,可以判断A错误,对于B、构造二次函数的图象,举出反例可得B错误,对于C、(1,2)是[0,3]的子集,由单调性的定义可得C正确,对于D、构造分段函数,举出反例可得D错误;即可得答案.解答:
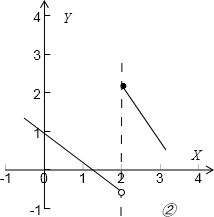
 解:根据题意,依次分析选项可得:
解:根据题意,依次分析选项可得:对于A、y=
 的定义域为x≠0,x取特殊值-1与1,有f(-1)=-4,f(4)=4,则f(-4)<f(4),故y=
的定义域为x≠0,x取特殊值-1与1,有f(-1)=-4,f(4)=4,则f(-4)<f(4),故y= 不是减函数,则A错误;
不是减函数,则A错误;对于B、如图①,其中的函数,有f(0)<f(2),而f(x)在[0,2]上不是单调的,B错误;
对于C、(1,2)是[0,3]的子集,则若f(x)在区间[0,3]上单调递减,则f(x)在(1,2)上单调递减,则C正确;
对于D、如图②,f(x)在区间(1,2),[2,3]上分别单调递减,但f(x)在(1,3]上不是单调,D错误;
故选C.
点评:本题考查函数的单调性的判断,关键是理解函数单调性的定义,并能举出反例.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 则下列结论正确的是( )
则下列结论正确的是( ) 为“三件产品全不是次品”,
为“三件产品全不是次品”, 为“三件产品全是次品”,
为“三件产品全是次品”, 为“三件产品不全是次品”,则下列结论正确的是:
为“三件产品不全是次品”,则下列结论正确的是: :
: ,
, ,那么下列结论正确的是( )
,那么下列结论正确的是( ) ,
, B.
B. ,
,
 D.
D.