题目内容
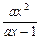
a<0时,原不等式的解集是(
 ,0);
,0);a=0时,原不等式的解集是(-∞,0);
a>0时,原不等式的解集是(-∞,0)∪(
 ,+∞)
,+∞)解法一:由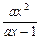 >x,得
>x,得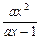 -x>0,即
-x>0,即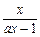 >0.
>0.
此不等式与x(ax-1)>0同解.
若a<0,则 <x<0;
<x<0;
若a=0,则x<0;
若a>0,则x<0或x> .
.
综上,a<0时,原不等式的解集是( ,0);
,0);
a=0时,原不等式的解集是(-∞,0);
a>0时,原不等式的解集是(-∞,0)∪( ,+∞)
,+∞)
解法二:由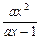 >x,得
>x,得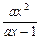 -x>0,即
-x>0,即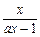 >0.
>0.
此不等式与x(ax-1)>0同解.
显然,x≠0.
(1)当x>0时,得ax-1>0.
若a<0,则x< ,与x>0矛盾,
,与x>0矛盾,
∴此时不等式无解;
若a=0,则-1>0,此时不等式无解;
若a>0,则x> .
.
(2)当x<0时,得ax-1<0.
若a<0,则x> ,得
,得 <x<0;
<x<0;
若a=0,则-1<0,得x<0;
若a>0,则x< ,得x<0.
,得x<0.
综上,a<0时,原不等式的解集是( ,0);
,0);
a=0时,原不等式的解集是(-∞,0);
a>0时,原不等式的解集是(-∞,0)∪( ,+∞)
,+∞)
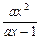 >x,得
>x,得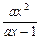 -x>0,即
-x>0,即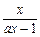 >0.
>0.此不等式与x(ax-1)>0同解.
若a<0,则
 <x<0;
<x<0;若a=0,则x<0;
若a>0,则x<0或x>
 .
.综上,a<0时,原不等式的解集是(
 ,0);
,0);a=0时,原不等式的解集是(-∞,0);
a>0时,原不等式的解集是(-∞,0)∪(
 ,+∞)
,+∞)解法二:由
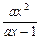 >x,得
>x,得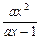 -x>0,即
-x>0,即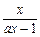 >0.
>0.此不等式与x(ax-1)>0同解.
显然,x≠0.
(1)当x>0时,得ax-1>0.
若a<0,则x<
 ,与x>0矛盾,
,与x>0矛盾,∴此时不等式无解;
若a=0,则-1>0,此时不等式无解;
若a>0,则x>
 .
.(2)当x<0时,得ax-1<0.
若a<0,则x>
 ,得
,得 <x<0;
<x<0;若a=0,则-1<0,得x<0;
若a>0,则x<
 ,得x<0.
,得x<0.综上,a<0时,原不等式的解集是(
 ,0);
,0);a=0时,原不等式的解集是(-∞,0);
a>0时,原不等式的解集是(-∞,0)∪(
 ,+∞)
,+∞)
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
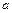 、
、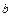 、
、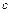 是三角形的边长,求证:
是三角形的边长,求证: ≥
≥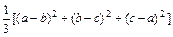
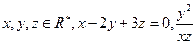 的最小值为 。
的最小值为 。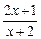 <0,试判断方程u2-2u+5-p2=0有无实根,并给出证明.
<0,试判断方程u2-2u+5-p2=0有无实根,并给出证明.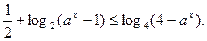
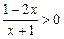 的解集是______。
的解集是______。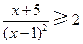 的解集是( )
的解集是( )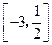
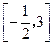
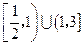
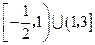
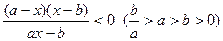
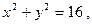 求
求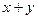 的最大值和最小值
的最大值和最小值