题目内容
若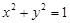 ,则
,则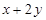 的最大值为______.
的最大值为______.
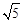 .
.
解析试题分析:解法一:(柯西不等式法)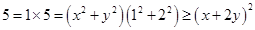 ,
, ,因此
,因此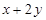 的最大值为
的最大值为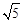 .
.
解法二:(几何法)令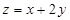 ,则直线
,则直线 与圆
与圆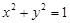 有公共点,圆心到直线的距离
有公共点,圆心到直线的距离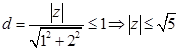 ,解得
,解得 ,因此
,因此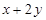 的最大值为
的最大值为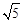 ;
;
解法三:(三角换元法)设 ,
,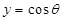 ,则
,则 ,其中
,其中
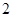 且
且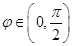 ,由于
,由于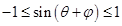 ,因此
,因此 ,即
,即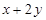 的最大值为
的最大值为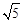 .
.
考点:1.柯西不等式;2.直线与圆的位关系;3.三角换元法

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=x2+ (x>0)的最小值是 ( )
(x>0)的最小值是 ( )
A.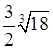 | B.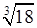 | C. | D.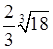 |
对于实数x,y,若|x-1|≤1,|y-2|≤1,则|x-2y+1|的最大值为 ( )
| A.5 | B.4 | C.8 | D.7 |
 对任意实数
对任意实数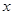 恒成立,则正实数
恒成立,则正实数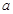 的取值范围 .
的取值范围 . ,且
,且 ,则
,则 的最小值为
的最小值为 
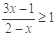 的解集是
的解集是 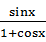 =
=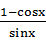 ”的证明过程:“等式两边同时乘以
”的证明过程:“等式两边同时乘以 得,左边=
得,左边=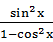 =
=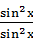 =1,右边=1,左边=右边,故原不等式成立”,应用了
=1,右边=1,左边=右边,故原不等式成立”,应用了