题目内容
不等式 对任意实数
对任意实数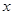 恒成立,则正实数
恒成立,则正实数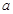 的取值范围 .
的取值范围 .
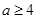
解析试题分析:因为不等式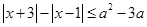 对任意实数
对任意实数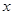 恒成立,所以
恒成立,所以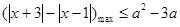 ,利用绝对值的几何意义可知
,利用绝对值的几何意义可知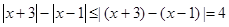 (当且仅当
(当且仅当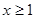 时等号成立),
时等号成立),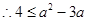 ,从中求解得到
,从中求解得到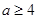 或
或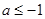 ,而
,而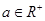 ,所以
,所以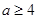 .
.
考点:1.恒成立问题;2.绝对值的三角不等式;3.二次不等式.

练习册系列答案
相关题目
下列三个不等式中:①a<0<b;②b<a<0;③b<0<a,其中能使 <
< 成立的充分条件有 ( )
成立的充分条件有 ( )
| A.①② | B.①③ | C.②③ | D.①②③ |
若关于x的不等式|x-2|+|x+3|<a的解集为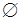 ,则实数a的取值范围为( )
,则实数a的取值范围为( )
| A.(-∞,1] | B.(-∞,1) |
| C.(-∞,5] | D.(-∞,5) |
若关于x的不等式|x-2|+|x-a|≥a在R上恒成立,则a的最大值是( ).
| A.0 | B.1 | C.-1 | D.2 |
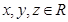 ,且
,且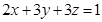 ,则
,则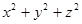 的最小值是 .
的最小值是 .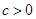 ,当非零实数a,b满足
,当非零实数a,b满足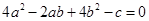 ,且使
,且使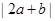 最大时,
最大时,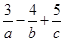 的最小值为 .
的最小值为 .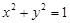 ,则
,则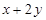 的最大值为______.
的最大值为______.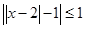 的解集为___________.
的解集为___________.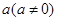 和
和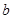 不等式
不等式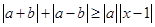 恒成立,则实数x的取值范围是_________.
恒成立,则实数x的取值范围是_________.