题目内容
16.设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=1,b1=2,a2+b3=10,a3+b2=7.(1)求数列{an},{bn}的通项公式;
(2)设数列{bn}的前n项和为Sn,记${c_n}=(1+\frac{S_n}{2})•{a_n},n∈{N^*}$,求数列{cn}的前n项和Tn.
分析 (1)利用等差数列与等比数列的通项公式即可得出;
(2)利用“错位相减法”、等比数列的通项公式与前n项和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,且a1=1,b1=2,a2+b3=10,a3+b2=7.
∴$\left\{\begin{array}{l}{{a}_{1}+d+{b}_{1}{q}^{2}=10}\\{{a}_{1}+2d+{b}_{1}q=7}\end{array}\right.$,即$\left\{\begin{array}{l}{1+d+2{q}^{2}=10}\\{1+2d+2q=7}\end{array}\right.$,
消去d得2q2-q-6=0,(2q+3)(q-2)=0,
∵{bn}是各项都为正数的等比数列,
∴q=2,d=1,
∴an=n,bn=2n.
(2)Sn=2n+1-2,…(7分)
cn=an•($\frac{Sn}{2}$+1)=n•2n,
设Tn=1•21+2•22+3•23+…+n•2n,
2Tn=1•22+2•23+…+(n-1)•2n+n•2n+1,
相减,可得Tn=(n-1)•2n+1+2.
点评 本题考查了等差数列与等比数列的通项公式与前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.已知函数f(x)满足f(x+1)=x2-1,则( )
| A. | f(x)=x2-2x | B. | f(x)=x2+2x | C. | f(x)=x2-4x | D. | f(x)=x2+4x |
7.已知全集U={1,2,3,4,5,6,7},集合A={1,3,4,6},B={2,4,5,6},则A∩(∁UB)=( )
| A. | {1,3} | B. | {2,5} | C. | {4} | D. | ∅ |
11.设a>1,b>1且ab-(a+b)=1,那么( )
| A. | ab有最大值$2\sqrt{2}+1$ | B. | ab有最小值${(\sqrt{2}+2)^2}$ | C. | ab有最小值${(\sqrt{2}+1)^2}$ | D. | ab有最大值$2(\sqrt{2}+1)$ |
5.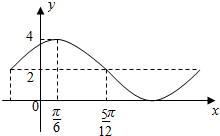 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )| A. | B=1 | B. | φ=$\frac{π}{6}$ | C. | ω=1 | D. | A=4 |