题目内容
如图,在 中,
中, 为
为 边上的高,
边上的高, ,沿
,沿 将
将 翻折,使得
翻折,使得 得几何体
得几何体
(1)求证: ; (2)求二面角
; (2)求二面角 的余弦值。
的余弦值。

【答案】
因为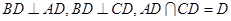 ,所以
,所以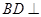 平面
平面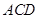 。
。
又因为 平面
平面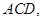 所以
所以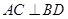 ①……… 1分
①……… 1分
在 中,
中,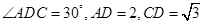 ,由余弦定理,
,由余弦定理,
得
因为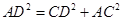 ,所以
,所以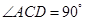 ,即
,即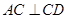 。② ……… 3分
。② ……… 3分
由①,②及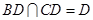 ,可得
,可得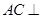 平面
平面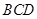 ………4分
………4分
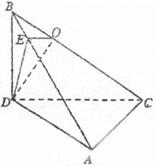
(2)在 中,过
中,过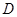 作
作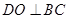 于
于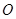 ,则
,则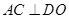 ,所以
,所以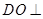 平面
平面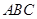
在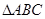 中,过
中,过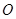 作
作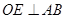 于
于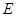 ,连
,连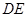 ,则
,则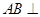 平面
平面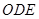 ,
,
所以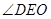 为二面角
为二面角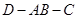 的平面角 ……… 6分
的平面角 ……… 6分
在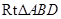 中,求得
中,求得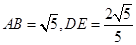 ,
,
在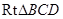 中,求得
中,求得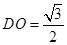 ,
,
所以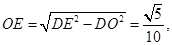 所以
所以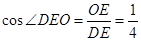 。
。
因此,所求二面角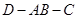 的余弦值为
的余弦值为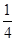 。
。
【解析】略

练习册系列答案
相关题目
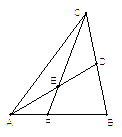
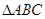 中,
中,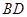 为
为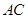 边上的高,
边上的高,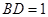 ,
,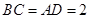 ,沿
,沿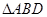 翻折,使得
翻折,使得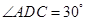 ,得到几何体
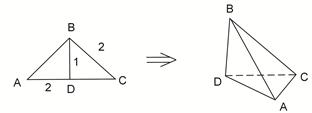
,得到几何体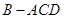 。
。
 ;
;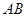 与平面
与平面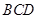 所成角的正切值。
所成角的正切值。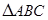 中,
中,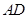 为
为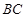 边上的中线,
边上的中线,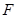 为
为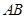 上任意一点,
上任意一点,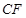 交
交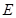 .求证:
.求证: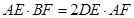 .
. 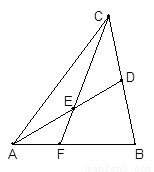
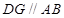 ,然后利用平行性得到相似比,
,然后利用平行性得到相似比,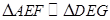 ,
,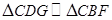 ,然后得到比例相等。充分利用比值问题转化得到结论。
,然后得到比例相等。充分利用比值问题转化得到结论。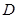 作
作 ,∴
,∴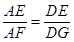 ,
,  , ∵
, ∵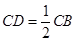 ,
,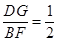 ,
,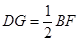 ,
,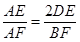 ,即
,即 中,
中,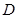 为
为 边上的中点,
边上的中点, ,
, 交
交 于点
于点 ,交
,交 延长线于点
延长线于点 ,若
,若 ,
,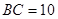 ,则
,则 的长为 .
的长为 .