题目内容
一货轮航行到M处,测得灯塔S在货轮的北偏东15°相距20里处,随后货轮按北偏西30°的方向航行,半小时后,又测得灯塔在货轮的北偏东45°处,则货轮的航行速度为________里/小时.
20( -
- )
)
分析:设半小时后到的点为N,依题意可知∠M,∠S,∠N,设NH=x,则MH=x,HS=20-x,进而在直角三角形NHS中利用tanS=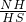 求得NH,进而求得MN.利用路程除以时间即可求得货船的速度.
求得NH,进而求得MN.利用路程除以时间即可求得货船的速度.
解答:货轮按北偏西30度的方向航行,半小时后到的点为N,△MNS中,∠M=45°,∠S=30°,∠N=105°,过N作NH垂直于MS,得两个特殊的直角三角形,设NH=x,则MH=x,HS=20-x,
tanS=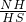 =
= =
= ,求得x=10(
,求得x=10( -1)
-1)
∴NM= x=10(
x=10( -
- )
)
∴货轮的航行速度为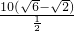 =20(
=20( -
- )里/每小时.
)里/每小时.
故答案为:20( -
- )
)
点评:本题主要考查了解三角形的实际应用.注意利用建立数学模型,充分利用数学知识来解决问题.
 -
- )
)分析:设半小时后到的点为N,依题意可知∠M,∠S,∠N,设NH=x,则MH=x,HS=20-x,进而在直角三角形NHS中利用tanS=
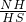 求得NH,进而求得MN.利用路程除以时间即可求得货船的速度.
求得NH,进而求得MN.利用路程除以时间即可求得货船的速度.解答:货轮按北偏西30度的方向航行,半小时后到的点为N,△MNS中,∠M=45°,∠S=30°,∠N=105°,过N作NH垂直于MS,得两个特殊的直角三角形,设NH=x,则MH=x,HS=20-x,
tanS=
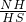 =
= =
= ,求得x=10(
,求得x=10( -1)
-1)∴NM=
 x=10(
x=10( -
- )
)∴货轮的航行速度为
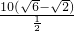 =20(
=20( -
- )里/每小时.
)里/每小时.故答案为:20(
 -
- )
)点评:本题主要考查了解三角形的实际应用.注意利用建立数学模型,充分利用数学知识来解决问题.

练习册系列答案
相关题目