Question

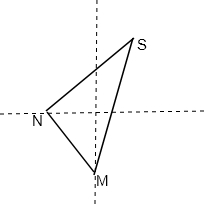
一货轮航行到M处，测得灯塔S在货轮北偏东15°相距20海里处，随后货轮按北偏西30°的方向航行，半小时后，又测得灯塔在北偏东45°，求货轮的速度．

Answer 1

分析：由题意知SM=20，∠SNM=105°，∠NMS=45°，∠MSN=30°，△MNS中利用正弦定理可得

MN

sin30°

=

20

sin105°

，代入可求MN，进一步利用速度公式即可

解答：解：由题意知SM=20，∠SNM=105°，∠NMS=45°，∴∠MSN=30°，
sin105°=sin（60°+45°）=sin60°cos45°+cos60°sin45°
=

3

2

×

2

2

+

1

2

×

2

2

=

6 + 2

4

在△MNS中利用正弦定理可得，

MN

sin30°

=

20

sin105°

，
∴为MN=

10

6 + 2 4

=10（

6

-

2

），
∴货轮的速度为

10( 6 - 2 )

1 2

=20（

6

-

2

）（海里/小时）
答：货轮的速度为20（

6

-

2

）海里/小时．

点评：本题主要考查了正弦定理在解三角形中的应用，解决实际问题的关键是要把实际问题转化为数学问题，然后利用数学知识进行求解．