题目内容
200辆汽车通过某一段公路时,时速的频率分布直方图如图所示,则时速在[50,70)的汽车大约有( ).
A:60辆 B:80辆 C:70辆 D:140辆
D
解析试题分析:因为,频率分布直方图中,频数÷样本容量=频率,所以,时速在[50,70)的汽车大约有200×(0.03+0.04)×10=140,故选D。
考点:本题主要考查频率分布直方图。
点评:简单题,矩形的高为频率、组距为底。频数÷样本容量=频率。

为了解一片速生林的生长情况,随机测量了其中100株树木的 底部周长(单位:cm).根据所得数据画出了样本的频率分布直方图,那么在这100株树木中,底部周长小于110cm的株数是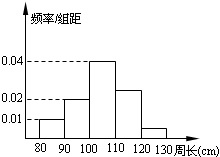
| A.80 | B.70 | C.60 | D.30 |
某班有50名同学,将其编为1、2、3、…、50号,并按编号从小到大平均分成5组.现用系统抽样方法,从该班抽取5名同学进行某项调查,若第1组抽取的学生编号为3,第2组抽取的学生编号为13,则第4组抽取的学生编号为
| A.14 | B.23 | C.33 | D.43 |
利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅下表来确定断言“X和Y有关系”的可信度。如果k>5.024,那么就有把握认为“X和Y有关系”的百分比为( )
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
某公司有员工49人,其中30岁以上的员工有14人,没超过30岁的员工有35人,为了解员工的健康情况,用分层抽样的方法抽一个容量为7的样本,其中30岁以上的员工应抽多少( )
| A.2人 | B.4人 | C.5人 | D.1人 |
在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟和效果最好的模型是( )
| A.模型1的相关指数R2为0.25 | B.模型2的相关指数R2为0.50 |
| C.模型3的相关指数R2为0.98 | D.模型4的相关指数R2为0.80 |
从2003件产品中选取50件,若采用下面的方法选取:先用简单随机抽样从2003件产品中剔除3件,剩下的2000件再按系统抽样的方法抽取,则每件产品被选中的概率
| A.不都相等 | B.都不相等 | C.都相等,且为 | D.都相等,且为 |
对变量 有观测数据(
有观测数据( ,
, )(
)( ),得散点图1;对变量
),得散点图1;对变量 有观测数据(
有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断
| A.变量x 与y 正相关,u 与v 正相关 | B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 | D.变量x 与y 负相关,u 与v 负相关 |


 的值为( )
的值为( )