题目内容
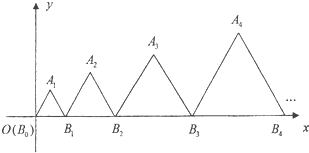 如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则
如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则| a |
| d |
分析:根据题意得,正三角形A1B0B1的边长为a,利用正三角形的性质得出点A1的坐标,又点A1落在抛物线y2=2px(p>0)上,则点A1的坐标适合抛物线方程,得到p=
a;又{an}是首项为a,公差为d的等差数列,同理得到点A2的坐标且点A2落在抛物线y2=2px(p>0)上,则有a=d,从而求出
的值.
| 3 |
| 4 |
| a |
| d |
解答:解:由题意得,正三角形A1B0B1的边长为a,
∴点A1的坐标为(
,
),
又∵点A1落在抛物线y2=2px(p>0)上,则(
)2=2p×
,
∴p=
a,
又{an}是首项为a,公差为d的等差数列,a2=a+d,
即正三角形A2B1B2的边长为a+d,
∴点A2的坐标为(a+
,
(a+d)),
又∵点A2落在抛物线y2=2px(p>0)上,则[
]2=2p(a+
),
化简得(a-d)(2a+d)=0,∵2a+d>0,
∴a=d,
则
的值为1.
故选A.
∴点A1的坐标为(
| a |
| 2 |
| ||
| 2 |
又∵点A1落在抛物线y2=2px(p>0)上,则(
| ||
| 2 |
| a |
| 2 |
∴p=
| 3 |
| 4 |
又{an}是首项为a,公差为d的等差数列,a2=a+d,
即正三角形A2B1B2的边长为a+d,
∴点A2的坐标为(a+
| a+d |
| 2 |
| ||
| 2 |
又∵点A2落在抛物线y2=2px(p>0)上,则[
| ||
| 2 |
| a+d |
| 2 |
化简得(a-d)(2a+d)=0,∵2a+d>0,
∴a=d,
则
| a |
| d |
故选A.
点评:本题主要考查数列与解析几何综合的知识点,本题是一道综合性的习题,解答本题的关键是准确求出正三角形的坐标后代入抛物线方程得出变量之间的关系式.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
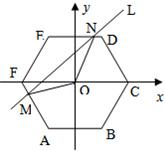 如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )
如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )| A、偶函数 | B、奇函数 | C、不是奇函数,也不是偶函数 | D、奇偶性与k有关 |
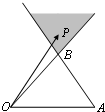 如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且
如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且 1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
 (2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是
(2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是