题目内容
已知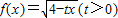 的定义域为A,不等式x2-4x-12<0的解集为B.记p:x∈A,q:x∈B
的定义域为A,不等式x2-4x-12<0的解集为B.记p:x∈A,q:x∈B(1)当t=2时,试判断p是q的什么条件?
(2)若p是q的必要不充分条件,求实数t的取值范围.
【答案】分析:(1)当t=2时,解不等式4-2x≥0,求出A={x|x≤2},解一元二次不等式x2-4x-12<0求出B={x|-2<x<6},由此能够得到命题p是命题q的必要不充分条件.
(2)由M={x|x<-3或x>5},N={x|(x-8)(x+a)≤0},命题p是命题q的必要不充分条件,分类讨论能够求出a的取值范围.
解答:解:(1)当t=2时,A={x|x≤2},
B={x|-2<x<6},
∵命题p:x∈A,命题q:x∈B,
∴q推不出p,p推不出q,
∴命题p是命题q的不必要不充分条件.
(2)∵A={x|4-tx≥0},
当t=0时,A=R,此时p是q的必要不充分条件;
当t>0时,A={x|x≤ },
},
要使得命题p是命题q的必要不充分条件,则 ≥6,解得0<t≤
≥6,解得0<t≤ ;
;
当t<0时,A={x|x≥ },
},
要使得命题p是命题q的必要不充分条件,则 ≤-2,解得-2≤t<0;
≤-2,解得-2≤t<0;
综上所述,t的取值范围是{a|-2≤t≤ }.
}.
点评:本题考查必要条件、充分条件、充要条件的性质和应用,是基础题.解题时要认真审题,仔细解答.
(2)由M={x|x<-3或x>5},N={x|(x-8)(x+a)≤0},命题p是命题q的必要不充分条件,分类讨论能够求出a的取值范围.
解答:解:(1)当t=2时,A={x|x≤2},
B={x|-2<x<6},
∵命题p:x∈A,命题q:x∈B,
∴q推不出p,p推不出q,
∴命题p是命题q的不必要不充分条件.
(2)∵A={x|4-tx≥0},
当t=0时,A=R,此时p是q的必要不充分条件;
当t>0时,A={x|x≤
 },
},要使得命题p是命题q的必要不充分条件,则
 ≥6,解得0<t≤
≥6,解得0<t≤ ;
;当t<0时,A={x|x≥
 },
},要使得命题p是命题q的必要不充分条件,则
 ≤-2,解得-2≤t<0;
≤-2,解得-2≤t<0;综上所述,t的取值范围是{a|-2≤t≤
 }.
}.点评:本题考查必要条件、充分条件、充要条件的性质和应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知函数y=3cos(2x+
) 的定义域为[a,b],值域为[-1,3],则b-a的值不可能是( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
| D、π |