题目内容
10.已知函数f(x)=$\left\{\begin{array}{l}{-\frac{1}{x-1},x<0}\\{(x-1)^{2},x≥0}\end{array}\right.$,若直线y=m与函数f(x)的图象有三个不同的交点,则实数m的取值范围(0,1).分析 作函数f(x)=$\left\{\begin{array}{l}{-\frac{1}{x-1},x<0}\\{(x-1)^{2},x≥0}\end{array}\right.$与直线y=m的图象,从而结合图象解得.
解答 解:作函数f(x)=$\left\{\begin{array}{l}{-\frac{1}{x-1},x<0}\\{(x-1)^{2},x≥0}\end{array}\right.$与直线y=m的图象如下,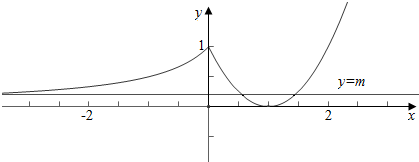 ,
,
由图象可知,
当m∈(0,1)时,直线y=m与函数f(x)的图象有三个不同的交点,
故答案为:(0,1).
点评 本题考查了函数的图象的作法及基本初等函数的应用,同时考查了数形结合的思想.

练习册系列答案
相关题目