题目内容
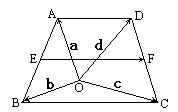
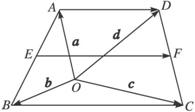
在梯形ABCD中，AB∥CD，AB=2CD，M，N分别是CD，AB的中点，设
=
，
=
．若
=m
+n
，则
=（ ）
| AB |
| a |
| AD |
| b |
| MN |
| a |
| b |
| n |
| m |
分析：根据题意，得到
=
且
=
，从而算出
=
+
，结合
=
-
得到
=
-
=m
+n
，由此可得m=
且n=-1，可得
的值．
| AN |
| 1 |
| 2 |
| AB |
| DM |
| 1 |
| 4 |
| AB |
| AM |
| AD |
| 1 |
| 4 |
| AB |
| MN |
| AN |
| AM |
| MN |
| 1 |
| 4 |
| a |
| b |
| a |
| b |
| 1 |
| 4 |
| n |
| m |
解答：解：∵梯形ABCD中，AB∥CD，AB=2CD，M，N分别是CD，AB的中点，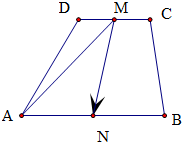
∴
=
，
=
=
∴
=
+
=
+
可得
=
-
=
-(
+
)=
-
∵
=
，
=
．∴
=
-
=m
+n
，
可得m=
，n=-1，
=
=-4
故选：B
∴
| AN |
| 1 |
| 2 |
| AB |
| DM |
| 1 |
| 2 |
| DC |
| 1 |
| 4 |
| AB |
∴
| AM |
| AD |
| DM |
| AD |
| 1 |
| 4 |
| AB |
可得
| MN |
| AN |
| AM |
| 1 |
| 2 |
| AB |
| AD |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AB |
| AD |
∵
| AB |
| a |
| AD |
| b |
| MN |
| 1 |
| 4 |
| a |
| b |
| a |
| b |
可得m=
| 1 |
| 4 |
| n |
| m |
| -1 | ||
|
故选：B
点评：本题在梯形中求向量的线性表达式，着重考查了梯形的性质、向量的加减法法则和平面向量基本定理及其意义等知识点，属于中档题．
练习册系列答案
口算能手系列答案
相关题目
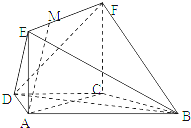如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，．∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上．
=a，
=b，
=c，
=d，E、F分别为AB、CD的中点，则下列表达中成立的是
=
(a＋b＋c＋d)
=a，
=b，
=c，
=d，E、F分别为AB、CD的中点，则下列表达中成立的是
=
(a＋b＋c＋d)
=a，
=b，
=c,
=d,E、F分别为AB、CD的中点，则下列表达中成立的是（ ）
=
（a+b+c+d） B.
=
（c+d-a-b）
=
（a+b-c-d） D.
=
（a-b+c-d）