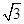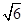题目内容
双曲线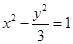 的左右两支上各有一点
的左右两支上各有一点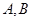 ,点
,点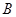 在直线
在直线 上的射影是点
上的射影是点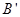 ,若直线
,若直线 过右焦点,则直线
过右焦点,则直线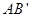 必过点( )
必过点( )
A.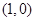 | B.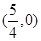 | C. | D.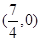 |
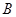
解析试题分析:根据双曲线的对称性可知,所求点必在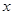 轴上(从选项来看也是如此),故可考虑特殊情况.设直线AB的方程为:
轴上(从选项来看也是如此),故可考虑特殊情况.设直线AB的方程为: .代入双曲线方程整理得:
.代入双曲线方程整理得: 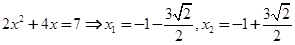 ,
,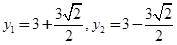 ,所以点
,所以点 ,
,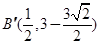 .
.
直线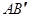 的方程为:
的方程为: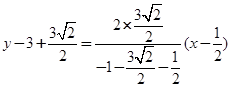 ,
,
令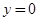 得:
得: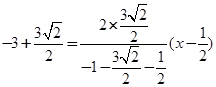 ,即
,即 ,
,
所以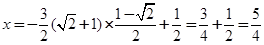 .
.
另法、当A点在无穷远处时,AB与渐近线平行,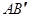 也与渐近线平行.这样求解,运算量更小.
也与渐近线平行.这样求解,运算量更小.
一般解法、设 ,代入双曲线方程得:
,代入双曲线方程得: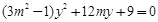 ,
,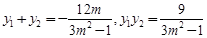 .直线
.直线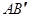 的方程为:
的方程为: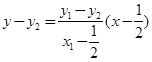 .
.
令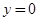 得:
得: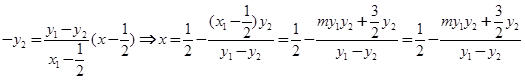 .
.
由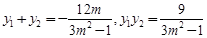 相除得:
相除得: ,所以
,所以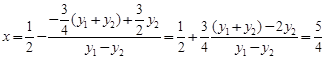
考点:直线与圆锥曲线的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
抛物线 的焦点为
的焦点为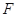 ,点
,点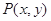 为该抛物线上的动点,又点
为该抛物线上的动点,又点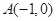 ,则
,则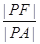 的最小值是( )
的最小值是( )
A.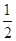 | B.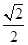 | C.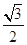 | D.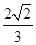 |
设双曲线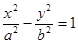
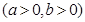 的虚轴长为2,焦距为
的虚轴长为2,焦距为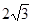 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.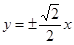 | B.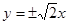 |
C.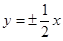 | D.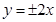 |
双曲线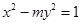 的一个焦点坐标为
的一个焦点坐标为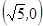 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.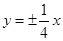 | B.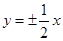 |
C.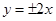 | D.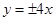 |
已知点M( ,0),椭圆
,0),椭圆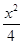 +y2=1与直线y=k(x+
+y2=1与直线y=k(x+ )交于点A、B,则△ABM的周长为( ).
)交于点A、B,则△ABM的周长为( ).
| A.4 | B.8 | C.12 | D.16 |
已知双曲线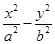 =1(a>0,b>0)的右焦点为F(2,0),设A,B为双曲线上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点O在以线段MN为直径的圆上,若直线AB斜率为
=1(a>0,b>0)的右焦点为F(2,0),设A,B为双曲线上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点O在以线段MN为直径的圆上,若直线AB斜率为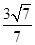 ,则双曲线离心率为( ).
,则双曲线离心率为( ).
A.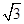 | B.2 | C.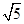 | D.4 |
已知双曲线的渐近线方程为y=±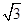 x,焦点坐标为(-4,0),(4,0),则双曲线方程为( ).
x,焦点坐标为(-4,0),(4,0),则双曲线方程为( ).
A.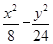 =1 =1 | B.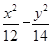 =1 =1 | C.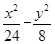 =1 =1 | D.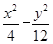 =1 =1 |
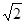
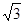
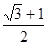
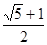
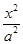 -y2=1(a>0)交于A,B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率是( ).
-y2=1(a>0)交于A,B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率是( ).