题目内容
不等式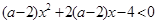 对于
对于 恒成立,那么
恒成立,那么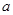 的取值范围是( )
的取值范围是( )
A.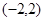 B.
B.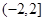 C.
C.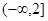 D.
D.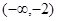
【答案】
B
【解析】
试题分析:因为要使得不等式 对于
对于 恒成立,那么要考虑当a-2=0时,即a=2,原不等式等价于-4<0显然恒成立,当a
恒成立,那么要考虑当a-2=0时,即a=2,原不等式等价于-4<0显然恒成立,当a 2时,则根据二次函数性质可知,只有开口向下,判别式小于零时满足题意,即
2时,则根据二次函数性质可知,只有开口向下,判别式小于零时满足题意,即 ,解得-2<a<2,综上可知参数a的范围是
,解得-2<a<2,综上可知参数a的范围是 ,故选B.
,故选B.
考点:本试题主要考查了含有参数的一元二次不等式的恒成立问题的运用。
点评:解决该试题的关键是要对参数a-2是否为零进行分类讨论,确定出不等式的性质,分别验证并求解得到结论。

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 对于
对于 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )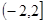 B.
B. C.
C.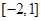 D.
D.
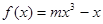 的图象上,以
的图象上,以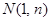 为切点的切线的倾斜角为
为切点的切线的倾斜角为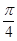 .
.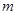 ,
,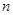 的值;
的值;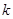 ,使得不等式
,使得不等式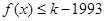 对于
对于 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数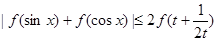 (
(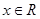 ,
,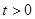 ).
). 对于
对于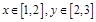 恒成立,求
恒成立,求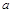 的取值范围”提出了各自的解题思路. 甲说:“可视
的取值范围”提出了各自的解题思路. 甲说:“可视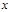 为变量,
为变量,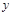 为常量来分析”; 乙说:“不等式两边同除以
为常量来分析”; 乙说:“不等式两边同除以 在R上单调递增,命题q:不等式
在R上单调递增,命题q:不等式
 恒成立,若“
恒成立,若“ ”为假,“
”为假,“ ”为真,求实数
”为真,求实数 的取值范围
的取值范围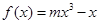 的图象上的点
的图象上的点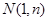 为切点的切线的倾斜角为
为切点的切线的倾斜角为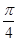 .
.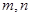 的值;
的值;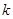 ,使不等式
,使不等式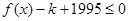 对于
对于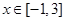 恒成立?若存在,求出最小的正整数
恒成立?若存在,求出最小的正整数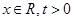 ,比较
,比较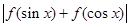 与
与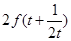 的大小.
的大小.