题目内容
求出一个数学问题的正确结论后,将其作为条件之一,提出与原来问题有关的新问题,我们把它称为原来问题的一个“逆向”问题.例如,原来问题是“若正四棱锥底面边长为4,侧棱长为3,求该正四棱锥的体积”.求出体积
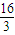 后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为
后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为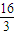 ,求侧棱长”;也可以是“若正四棱锥的体积为
,求侧棱长”;也可以是“若正四棱锥的体积为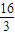 ,求所有侧面面积之和的最小值”.
,求所有侧面面积之和的最小值”.试给出问题“在平面直角坐标系xoy中,求点P(2,1)到直线3x+4y=0的距离.”的一个有意义的“逆向”问题,并解答你所给出的“逆向”问题.
【答案】分析:利用逆向”问题的意义可以是:(1)求到直线3x+4y=0的距离为2的点的轨迹方程.或者 (2)若点P(2,1)到直线l:ax+by=0的距离为2,求直线l的方程.利用点到直线的距离公式即可得出.
解答:解:点(2,1)到直线3x+4y=0的距离为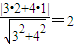 .
.
“逆向”问题可以是:(1)求到直线3x+4y=0的距离为2的点的轨迹方程.
设所求轨迹上任意一点为P(x,y),则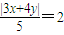 ,
,
所求轨迹为3x+4y-10=0或3x+4y+10=0.
(2)若点P(2,1)到直线l:ax+by=0的距离为2,求直线l的方程.
由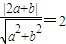 ,化简得4ab-3b2=0,b=0或4a=3b,
,化简得4ab-3b2=0,b=0或4a=3b,
所以,直线l的方程为x=0或3x+4y=0.
点评:正确理解逆向”问题的意义和点到直线的距离公式是解题的关键.
解答:解:点(2,1)到直线3x+4y=0的距离为
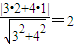 .
. “逆向”问题可以是:(1)求到直线3x+4y=0的距离为2的点的轨迹方程.
设所求轨迹上任意一点为P(x,y),则
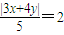 ,
,所求轨迹为3x+4y-10=0或3x+4y+10=0.
(2)若点P(2,1)到直线l:ax+by=0的距离为2,求直线l的方程.
由
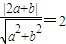 ,化简得4ab-3b2=0,b=0或4a=3b,
,化简得4ab-3b2=0,b=0或4a=3b,所以,直线l的方程为x=0或3x+4y=0.
点评:正确理解逆向”问题的意义和点到直线的距离公式是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为
后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为 的直线交抛物线C:y2=2px(p>0)于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过焦点F.
的直线交抛物线C:y2=2px(p>0)于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过焦点F.