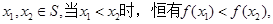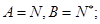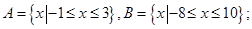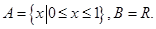题目内容
设S,T是R的两个非空子集,如果存在一个从S到T的函数y=f(x)满足:(i)T={f(x)|x∈S};(ii)对任意x1,x2∈S,当x1<x2时,恒有f(x1)<f(x2),那么称这两个集合“保序同构”,现给出以下3对集合:
①A=N,B=N*;
②A={x|-1≤x≤3},B={x|-8≤x≤10};
③A={x|0≤x≤1},B=R.
其中,“保序同构”的集合对的序号是 .(写出“保序同构”的集合对的序号).
【答案】分析:本题考查的是函数的性质,由题意可知S为函数的一个定义域,T为其所对应的值域,且函数y=f(x)为单调增函数,
对题目给出的三个命题中的集合对逐一分析看是否能找到这样的函数y=f(x)即可.
解答:解:对于命题①中的两个集合,可取函数f(x)=2x,x∈N,是“保序同构”;
对于命题②中的两个集合,可取函数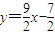 (-1≤x≤3),是“保序同构”;
(-1≤x≤3),是“保序同构”;
对于命题③中的两个集合,可取函数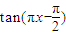 (0≤x≤1),是“保序同构”.
(0≤x≤1),是“保序同构”.
故答案为①②③.
点评:本题考查了命题的真假判断与应用,考查了子集与交集、并集运算的转换,考查了函数值域的求法,解答此题的关键是明白新定义“保序同构”指的是什么意思,是基础题.
对题目给出的三个命题中的集合对逐一分析看是否能找到这样的函数y=f(x)即可.
解答:解:对于命题①中的两个集合,可取函数f(x)=2x,x∈N,是“保序同构”;
对于命题②中的两个集合,可取函数
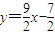 (-1≤x≤3),是“保序同构”;
(-1≤x≤3),是“保序同构”;对于命题③中的两个集合,可取函数
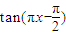 (0≤x≤1),是“保序同构”.
(0≤x≤1),是“保序同构”.故答案为①②③.
点评:本题考查了命题的真假判断与应用,考查了子集与交集、并集运算的转换,考查了函数值域的求法,解答此题的关键是明白新定义“保序同构”指的是什么意思,是基础题.

练习册系列答案
相关题目
 满足:
满足: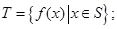 (ii)对任意
(ii)对任意