题目内容
已知数列{an}中,对一切自然数n,都有an∈(0,1)且an•an+12+2an+1-an=0.求证:
(1)an+1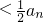 Sn;
Sn;
(2)若Sn表示数列{an}的前n项之和,则Sn<2a1.
解:(1)由已知an•an+12+2an+1-an=0得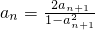 ,
,
又因为an∈(0,1),所以0<1-an+12<1,因此an>2an+1,即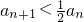 (6分)
(6分)
(2)由结论(1)可知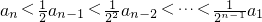 ,即
,即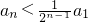 ,
,
于是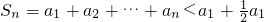
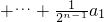 =
= ,
,
即Sn<2a1(14分)
分析:(1)通过对已知等式变形分离出an,利用an∈(0,1),得到要证的不等式.
(2)由(1)先对前n项和放缩,再利用等比数列的前n项和公式求和,得到要证的不等式.
点评:证明不等式常用到通过放缩法得到要证的不等式,利用等比数列的前n项和公式注意判断公比是否为1.
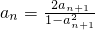 ,
,又因为an∈(0,1),所以0<1-an+12<1,因此an>2an+1,即
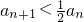 (6分)
(6分)(2)由结论(1)可知
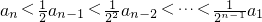 ,即
,即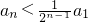 ,
,于是
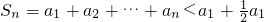
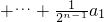 =
= ,
,即Sn<2a1(14分)
分析:(1)通过对已知等式变形分离出an,利用an∈(0,1),得到要证的不等式.
(2)由(1)先对前n项和放缩,再利用等比数列的前n项和公式求和,得到要证的不等式.
点评:证明不等式常用到通过放缩法得到要证的不等式,利用等比数列的前n项和公式注意判断公比是否为1.

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|