题目内容
(2013•重庆)在△ABC中,内角A,B,C的对边分别是a,b,c,且a2+b2+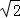 ab=c2.
ab=c2.
(1)求C;
(2)设cosAcosB=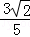 ,
,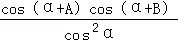 =
= ,求tanα的值.
,求tanα的值.
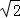 ab=c2.
ab=c2.(1)求C;
(2)设cosAcosB=
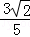 ,
,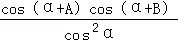 =
= ,求tanα的值.
,求tanα的值.(1) (2)tanα=1或tanα=4
(2)tanα=1或tanα=4
 (2)tanα=1或tanα=4
(2)tanα=1或tanα=4(1)∵a2+b2+ ab=c2,即a2+b2﹣c2=﹣
ab=c2,即a2+b2﹣c2=﹣ ab,
ab,
∴由余弦定理得:cosC= =
= =﹣
=﹣ ,
,
又C为三角形的内角,
则C= ;
;
(2)由题意 =
= =
= ,
,
∴(cosA﹣tanαsinA)(cosB﹣tanαsinB)= ,
,
即tan2αsinAsinB﹣tanα(sinAcosB+cosAsinB)+cosAcosB=tan2αsinAsinB﹣tanαsin(A+B)+cosAcosB= ,
,
∵C= ,A+B=
,A+B= ,cosAcosB=
,cosAcosB= ,
,
∴sin(A+B)= ,cos(A+B)=cosAcosB﹣sinAsinB=
,cos(A+B)=cosAcosB﹣sinAsinB= ﹣sinAsinB=
﹣sinAsinB= ,即sinAsinB=
,即sinAsinB= ,
,
∴ tan2α﹣
tan2α﹣ tanα+
tanα+ =
= ,即tan2α﹣5tanα+4=0,
,即tan2α﹣5tanα+4=0,
解得:tanα=1或tanα=4.
 ab=c2,即a2+b2﹣c2=﹣
ab=c2,即a2+b2﹣c2=﹣ ab,
ab,∴由余弦定理得:cosC=
 =
= =﹣
=﹣ ,
,又C为三角形的内角,
则C=
 ;
;(2)由题意
 =
= =
= ,
,∴(cosA﹣tanαsinA)(cosB﹣tanαsinB)=
 ,
,即tan2αsinAsinB﹣tanα(sinAcosB+cosAsinB)+cosAcosB=tan2αsinAsinB﹣tanαsin(A+B)+cosAcosB=
 ,
,∵C=
 ,A+B=
,A+B= ,cosAcosB=
,cosAcosB= ,
,∴sin(A+B)=
 ,cos(A+B)=cosAcosB﹣sinAsinB=
,cos(A+B)=cosAcosB﹣sinAsinB= ﹣sinAsinB=
﹣sinAsinB= ,即sinAsinB=
,即sinAsinB= ,
,∴
 tan2α﹣
tan2α﹣ tanα+
tanα+ =
= ,即tan2α﹣5tanα+4=0,
,即tan2α﹣5tanα+4=0,解得:tanα=1或tanα=4.

练习册系列答案
相关题目
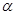 为第三象限角,
为第三象限角,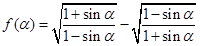 .
.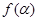 ;
;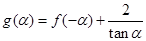 ,求函数
,求函数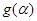 的最小值,并求取最小值时的
的最小值,并求取最小值时的 π,cos
π,cos )的值为________.
)的值为________. +
+

 ,
, ,求
,求
 ,
, ,则
,则 = .
= .  ,
,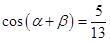 ,
,  .
.  为第二象限角,且
为第二象限角,且 ,求
,求 的值.
的值. +
+ i是纯虚数,则tan
i是纯虚数,则tan =( )
=( )
