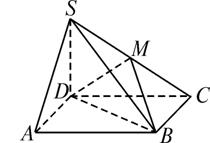
题目内容
如图，ABCD是平行四边形，S是平面ABCD外一点，M为SC的中点.
求证：SA∥平面MDB.
参考答案与解析:解析：要说明SA∥平面MDB，就要在平面MDB内找一条直线与SA平行，注意到M是SC的中点，于是可找AC的中点，构造与SA平行的中位线，再说明此中位线在平面MDB内，即可得证.
证明：连结AC交BD于N，因为ABCD是平行四边形，所以N是AC的中点.又因为M是SC的中点，所以MN∥SA.因为MN
平面MDB，所以SA∥平面MDB.
主要考察知识点:空间直线和平面
练习册系列答案
相关题目
