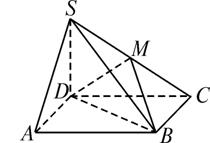
题目内容
如图,ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点.
求证:SA∥平面MDB.
思路解析:要说明SA∥平面MDB,只需在平面MDB内找一条直线与SA平行,注意到M是SC的中点,于是可找AC的中点,构造与SA平行的中位线,再说明此中位线在平面MDB内,即可得证.
证明:连结AC交BD于N,因为ABCD是平行四边形,所以N是AC的中点.又因为M是SC的中点,所以MN∥SA.因为MN![]() 平面MDB,所以SA∥平面MDB.
平面MDB,所以SA∥平面MDB.
方法归纳 证明与平行相关的几何问题的一般思路是由求证联想判定,由已知联想性质,从两头向中间推想,寻找它们的交汇点,从而使问题得证.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目