题目内容
已知F1、F2为双曲线 (a>0,b>0)的焦点,过F2作垂直于x轴的直线交双曲线于点P,且∠PF1F2=30°.求双曲线的离心率.
(a>0,b>0)的焦点,过F2作垂直于x轴的直线交双曲线于点P,且∠PF1F2=30°.求双曲线的离心率.
【答案】
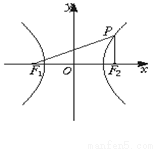
解:(1)设F2(c,0)(c>0),P(c,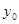 ),
),
则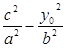 =1.解得
=1.解得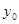 =±
=±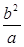 ,
,
∴|PF2|=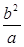 ,在
,在 PF2F1中,∠PF1F2=30°
PF2F1中,∠PF1F2=30°
|F1F2|= |PF2|,即
|PF2|,即
将c2=a2+b2代入,解得b2=2a2 ∴
故所求双曲线的离心率
【解析】略

练习册系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )