题目内容
9.随机地从区间[0,1]任取两数,分别记为x、y,则x2+y2≤1的概率P=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
分析 在平面直角坐标系中作出图形,则x,y∈[0,1]的平面区域为边长为1的正方形,符合条件x2+y2≤1的区域为以原点为圆心,1为半径的扇形内部,则扇形面积与正方形面积的比为概率.
解答 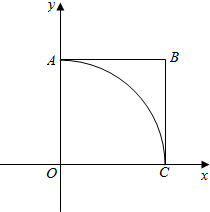 解:在平面直角坐标系中作出图形,如图所示,则x,y∈[0,1]的平面区域为边长为1的正方形OABC,
解:在平面直角坐标系中作出图形,如图所示,则x,y∈[0,1]的平面区域为边长为1的正方形OABC,
符合条件x2+y2≤1的区域为以原点为圆心,1为半径的扇形OAC内部,
∴P(x2+y2≤1)=$\frac{{S}_{扇形OAC}}{{S}_{正方形OABC}}$=$\frac{π}{4}$.
故选:C.
点评 本题考查了几何概型的概率计算,正确作出几何图形是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
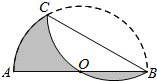 如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是$\frac{8π}{3}$.(结果保留π)
如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是$\frac{8π}{3}$.(结果保留π)