题目内容
19.下列四个命题:(1)函数f(x)在(0,+∞)上单调递增,在(-∞,0)上也单调递增,所以f(x)在(-∞,0)∪(0,+∞)上是增函数;
(2)若函数f(x)=ax2+bx+2与x轴没有交点,则b2-8a<0;
(3)符合条件{1}⊆A⊆{1,2,3}的集合A有4个;
(4)函数f(x)=$\left\{\begin{array}{l}{lnx-{x}^{2}+2x(x>0)}\\{4x+1(x≤0)}\end{array}\right.$有3个零点.
其中正确命题的序号是(3)(4).
分析 举例说明(1)(2)错误;求出满足{1}⊆A⊆{1,2,3}的集合A判断(3);
要求f(x)=$\left\{\begin{array}{l}{lnx-{x}^{2}+2x(x>0)}\\{4x+1(x≤0)}\end{array}\right.$的零点个数,只要分别判断函数h(x)=lnx-x2+2x(x>0),与g(x)=4x+1(x≤0)的零点个数,再求和即可.
解答 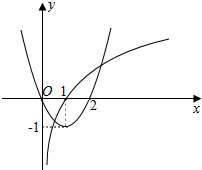 解:对于(1),函数f(x)在(0,+∞)上单调递增,在(-∞,0)上也单调递增,但f(x)在(-∞,0)∪(0,+∞)上不一定是增函数,
解:对于(1),函数f(x)在(0,+∞)上单调递增,在(-∞,0)上也单调递增,但f(x)在(-∞,0)∪(0,+∞)上不一定是增函数,
如f(x)=-$\frac{1}{x}$,故(1)错误;
对于(2),当a=b=0时,函数f(x)=ax2+bx+2=2,与x轴没有交点,b2-8a=0,故(2)错误;
对于(3),符合条件{1}⊆A⊆{1,2,3}的集合A有{1},{1,2},
{1,3},{1,2,3}共4个,故(3)正确;
对于(4),由f(x)=0可得lnx-x2+2x=0(x>0),或4x+1=0(x≤0).
由4x+1=0得x=-$\frac{1}{4}$,故g(x)=4x+1(x≤0)的零点个数为1,
由lnx-x2+2x=0得lnx=x2-2x,令y=lnx,y=x2-2x(x>0),
作出函数y=lnx,y=x2-2x(x>0)的图象,结合函数的图象可知,y=lnx,y=x2-2x(x>0)的图象有2个交点,
即函数f(x)=$\left\{\begin{array}{l}{lnx-{x}^{2}+2x(x>0)}\\{4x+1(x≤0)}\end{array}\right.$的零点个数是3,故(4)正确.
故答案为:(3)(4).
点评 本题考查命题的真假判断与应用,考查了函数单调性的性质,训练了函数零点的判定方法,是中档题.

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
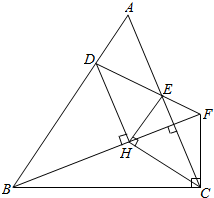 如图,设H为锐角△ABC的垂心,过点H作BH的垂线,与AB交于D,过点H作CH的垂线,与AC交于点E,点C作BC的垂线,与直线DE交于点F,证明FH=FC.
如图,设H为锐角△ABC的垂心,过点H作BH的垂线,与AB交于D,过点H作CH的垂线,与AC交于点E,点C作BC的垂线,与直线DE交于点F,证明FH=FC.