题目内容

已知直线l₁：ax+2y+6=0，直线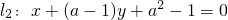 $数学公式$ ．
（1）若l₁⊥l₂，求a的值；
（2）若l₁∥l₂，求a的值．

解：（1）l₁⊥l₂时，a×1+2×（a-1）=0，
解得a= $\text{[math]}$ ．
∴a= $\text{[math]}$ ．
（2）∵a=1时，l₁不平行l₂，
∴l1∥l2? $\text{[math]}$ ，
解得a=-1．
分析：（1）当两条直线垂直时，斜率之积等于-1，解方程求出a的值．
（2）利用两直线平行时，一次项系数之比相等，但不等于常数项之比，求出a的值．
点评：本题考查两直线相交、垂直、平行、重合的条件，体现了转化的数学思想．属于基础题．

练习册系列答案

专项突破系列答案

初中文言文全能达标系列答案

新课标初中英语同步听读训练系列答案

新概念阅读延边大学出版社系列答案

走进文言文系列答案

新编中考英语短文填空阅读系列答案

通城学典周计划课外阅读训练系列答案

同步时间初中英语阅读系列答案

文言文教材全解系列答案

阅读训练80篇系列答案

相关题目

已知直线l₁：ax+2y+6=0和直线l₂：x+（a-1）y+a²-1=0，l₁⊥l₂，求a．

下列结论：
①若命题p：?x∈R，tanx=1；命题q：?x∈R，x²-x+1＞0．则命题“p∧?q”是假命题．
②已知直线l₁：ax+3y-1=0，l₂：x+by+1=0，则l₁⊥l₂的充要条件是

=-3．
③命题“若x²-3x+2=0，则x=1”的逆否命题为：“若x≠1，则x²-3x+2≠0”．
④任意的锐角三角形ABC中，有sinA＞cosB成立；
⑤直线x=

是函数y=2sin(2x-

)的图象的一条对称轴
其中正确结论的序号为

．（把你认为正确的命题序号都填上）

已知直线l₁：ax+3y+1=0，l₂：x+（a-2）y+a=0．当l₁∥l₂时，实数a的值为

已知直线l₁：ax-y+1=0与l₂：x+ay+1=0（a∈R），给出如下结论：
①不论a为何值时，l₁与l₂都互相垂直；
②不论a为何值时，l₁与l₂都关于直线x+y=0对称；
③当a变化时，l₁与l₂分别经过定点A（0，1）和B（-1，0）；
④当a变化时，l₁与l₂的交点轨迹是以AB为直径的圆（除去原点）．
其中正确的结论有

．（把你认为正确结论的序号都填上）

（2010•马鞍山模拟）给出下列四个结论：
①命题''?x∈R，x²-x＞0''的否定是''?x∈R，x²-x≤0''
②“若am²＜bm²，则a＜b”的逆命题为真；
③已知直线l₁：ax+2y-1=0，l₁：x+by+2=0，则l₁⊥l₂的充要条件是

=-2；
④对于任意实数x，有f（-x）=-f（x），g（-x）=g（x）且x＞0时，f'（x）＞0，g'（x）＞0，则x＜0时，f'（x）＞g'（x）．
其中正确结论的序号是

（填上所有正确结论的序号）