题目内容
8.下列函数是奇函数的是( )| A. | f(x)=(x-1)$\sqrt{\frac{1+x}{1-x}}$ | B. | f(x)=$\frac{|x|}{x}$ | ||
| C. | f(x)=$\left\{\begin{array}{l}{1+x,(x≥0)}\\{1-x(x<0)}\end{array}\right.$ | D. | f(x)=$\frac{1}{x-1}$ |
分析 根据函数奇偶性的定义进行判断即可.
解答 解:A.由$\frac{1+x}{1-x}$≥0得-1≤x<1,函数的定义域关于原点不对称,故f(x)为非奇非偶函数.
B.函数的定义域为(-∞,0)∪(0,+∞),f(-x)=$\frac{|x|}{-x}$=-$\frac{|x|}{x}$=-f(x),故f(x)为奇函数.
C.f(1)=1+1=2,f(-1)=1-(-1)=2.则f(-1)=f(1),则f(x)不是奇函数.
D.函数的定义域为(-∞,1)∪(1,+∞),函数的定义域关于原点不对称,故f(x)为非奇非偶函数.
故选:B.
点评 本题主要考查函数奇偶性的判断,根据函数奇偶性的定义结合函数定义域是否关于原点对称是解决本题的关键.

练习册系列答案
相关题目
18.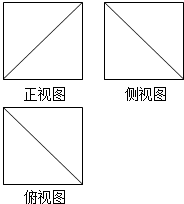 已知某几何体的三视图都是边长为6的正方形,如图所示,则该几何体的体积是( )
已知某几何体的三视图都是边长为6的正方形,如图所示,则该几何体的体积是( )
 已知某几何体的三视图都是边长为6的正方形,如图所示,则该几何体的体积是( )
已知某几何体的三视图都是边长为6的正方形,如图所示,则该几何体的体积是( )| A. | 180 | B. | 144 | C. | 92 | D. | 180或144 |
19.已知⊙O1与⊙O2的半径分别为R、r,且它们是方程x2-9x+14=0的两根,若⊙O1与⊙O2相切,则圆心距O1O2等于( )
| A. | 5 | B. | 9 | C. | 5或9 | D. | 10或18 |
17.在复平面内,复数z和$\frac{1+i}{1-2i}$所表示的点关于虚轴对称,则z=( )
| A. | -$\frac{1}{5}$+$\frac{3}{5}$i | B. | $\frac{1}{5}$+$\frac{3}{5}$i | C. | $\frac{1}{5}$-$\frac{3}{5}$i | D. | -$\frac{1}{5}$-$\frac{3}{5}$i |
 如图,点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,过点F的直线的斜率为3,与双曲线交于P,Q两点,分别过P、Q向右准线作垂线,垂足分别为M,N,且$\overrightarrow{PM}$=3$\overrightarrow{QN}$,求双曲线的离心率的大小.
如图,点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,过点F的直线的斜率为3,与双曲线交于P,Q两点,分别过P、Q向右准线作垂线,垂足分别为M,N,且$\overrightarrow{PM}$=3$\overrightarrow{QN}$,求双曲线的离心率的大小.