题目内容
18．
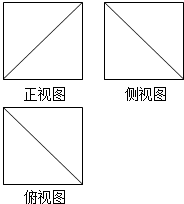已知某几何体的三视图都是边长为6的正方形，如图所示，则该几何体的体积是（ ）| A． | 180 | B． | 144 | C． | 92 | D． | 180或144 |
分析 把三视图转换成立体图，利用几何体的体积公式求出结果即可．
解答 解：根据三视图知：该几何体可能有两种情况，如图所示：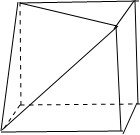
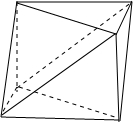
该几何体为棱长为6的正方体去掉一个三棱锥或去掉两个三棱锥，
且三棱锥的体积为$\frac{1}{3}$×$\frac{1}{2}$×62×6=36，
∴几何体的体积为63-36=180或63-36×2=144．
故选：D．
点评 本题考查了三视图和立体图之间的相互转换以及几何体的体积计算问题．也考查了空间想象能力的应用问题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
9．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一个焦点为F，若双曲线上存在点A使△AOF为正三角形，则双曲线C的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{3}+1$ | D． | $\sqrt{2}$+1 |
3．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上单调递增．若实数a满足f（log2a）+f（${log_{\frac{1}{2}}}a$）≤2f（2），则a的取值范围是（ ）
| A． | （-∞，4] | B． | （0，4] | C． | $（0，\frac{1}{4}]$ | D． | $[\frac{1}{4}，4]$ |
10．已知函数y=$\sqrt{1-x}$+$\sqrt{x+3}$的最大值为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\sqrt{2}$ | C． | 2 | D． | 2$\sqrt{2}$ |
8．下列函数是奇函数的是（ ）
| A． | f（x）=（x-1）$\sqrt{\frac{1+x}{1-x}}$ | B． | f（x）=$\frac{|x|}{x}$ | ||
| C． | f（x）=$\left\{\begin{array}{l}{1+x，（x≥0）}\\{1-x（x＜0）}\end{array}\right.$ | D． | f（x）=$\frac{1}{x-1}$ |