题目内容
设椭圆C: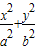 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为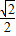 ,过原点O斜率为1的直线l与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为
,过原点O斜率为1的直线l与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为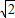 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)设P是椭圆上异于M,N外的一点,当直线PM,PN的斜率存在且不为零时,记直线PM的斜率为k1,直线PN的斜率为k2,试探究k1•k2是否为定值?若是,求出定值;若不是,说明理由.
【答案】分析:(I)设椭圆的焦距为2c(c>0),F(c,0),直线l:x-y=0,F到l的距离为 ,解得c,进一步求得a,b的值,从而写出椭圆C的方程;
,解得c,进一步求得a,b的值,从而写出椭圆C的方程;
(Ⅱ)由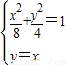 解得
解得 ,或
,或 ,表示出直线PM和PN的斜率,求的两直线斜率乘积的表达式,把y和x的表达式代入发现结果与p无关.
,表示出直线PM和PN的斜率,求的两直线斜率乘积的表达式,把y和x的表达式代入发现结果与p无关.
解答:解:(I)设椭圆的焦距为2c(c>0),F(c,0),直线l:x-y=0,F到l的距离为 ,解得c=2.又∵
,解得c=2.又∵ ,∴
,∴ ,∴b=2.
,∴b=2.
∴椭圆C的方程为 .(6分)
.(6分)
(Ⅱ)由 解得
解得 ,或
,或 ,
,
不妨设 ,P(x,y),
,P(x,y),
∴ ,
,
由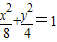 ,即x2=8-2y2,代入化简得
,即x2=8-2y2,代入化简得 为定值.(12分)
为定值.(12分)
点评:本题主要考查了圆锥曲线的共同特征.考查了学生综合分析问题和解决问题的能力.
 ,解得c,进一步求得a,b的值,从而写出椭圆C的方程;
,解得c,进一步求得a,b的值,从而写出椭圆C的方程;(Ⅱ)由
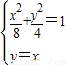 解得
解得 ,或
,或 ,表示出直线PM和PN的斜率,求的两直线斜率乘积的表达式,把y和x的表达式代入发现结果与p无关.
,表示出直线PM和PN的斜率,求的两直线斜率乘积的表达式,把y和x的表达式代入发现结果与p无关.解答:解:(I)设椭圆的焦距为2c(c>0),F(c,0),直线l:x-y=0,F到l的距离为
 ,解得c=2.又∵
,解得c=2.又∵ ,∴
,∴ ,∴b=2.
,∴b=2.∴椭圆C的方程为
 .(6分)
.(6分)(Ⅱ)由
 解得
解得 ,或
,或 ,
,不妨设
 ,P(x,y),
,P(x,y),∴
 ,
,由
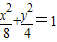 ,即x2=8-2y2,代入化简得
,即x2=8-2y2,代入化简得 为定值.(12分)
为定值.(12分)点评:本题主要考查了圆锥曲线的共同特征.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
相关题目
 +
+ =1(a>b>0)的左焦点为F1=(-
=1(a>b>0)的左焦点为F1=(- ,0),椭圆过点P(-
,0),椭圆过点P(- ,
, )
) =1(a>b>0)的左、右焦点分别为F1、F2,离心率为
=1(a>b>0)的左、右焦点分别为F1、F2,离心率为 ,左焦点F1到直线l:
,左焦点F1到直线l: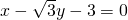 的距离等于长半轴长.
的距离等于长半轴长.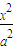 +
+ =1(a>b>0)过点M(1,1),离心率e=
=1(a>b>0)过点M(1,1),离心率e= ,O为坐标原点.
,O为坐标原点. •
• 为定值.
为定值. 设椭圆C:
设椭圆C: +
+ =1(a>b>0)的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
=1(a>b>0)的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且 =
=
 .
. y+3=0相切,求椭圆C的方程.
y+3=0相切,求椭圆C的方程. +
+ =1(a>b>0)的左焦点为F1=(-
=1(a>b>0)的左焦点为F1=(- ,0),椭圆过点P(-
,0),椭圆过点P(- ,
, )
)