题目内容
 设椭圆C:
设椭圆C: +
+ =1(a>b>0)的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
=1(a>b>0)的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且 =
=
 .
.(1)求椭圆C的离心率;
(2)若过A、Q、F三点的圆恰好与直线l:x+
 y+3=0相切,求椭圆C的方程.
y+3=0相切,求椭圆C的方程.
【答案】分析:(1)设出Q点坐标,由F,A的坐标表示出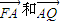 ,根据
,根据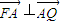 得出
得出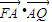 =0看,进而求得x,设P(x1,y1)根据
=0看,进而求得x,设P(x1,y1)根据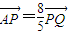 求得x1和y1的表达式,把点P的坐标代入椭圆方程进而求得a和c的关系,则椭圆的离心率可得.
求得x1和y1的表达式,把点P的坐标代入椭圆方程进而求得a和c的关系,则椭圆的离心率可得.
(2)根据(1)中a和c的关系可知F和Q的坐标,△AQF的外接圆圆心和半径,进而根据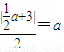 求得a,进而根据a和b,c的关系求得b,则椭圆的方程可得.
求得a,进而根据a和b,c的关系求得b,则椭圆的方程可得.
解答:解:(1)设Q(x,0),由F(-c,0)A(0,b)知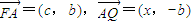
∵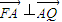 ,∴
,∴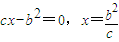
设P(x1,y1),
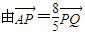 得
得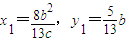
因为点P在椭圆上,所以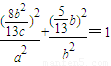
整理得2b2=3ac,即2(a2-c2)=3ac,2e2+3e-2=0,故椭圆的离心率e= .
.
(2)由(1)知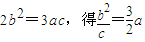 ,
,
于是F(- a,0)Q
a,0)Q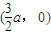 ,
,
△AQF的外接圆圆心为( a,0),半径r=
a,0),半径r= |FQ|=a
|FQ|=a
所以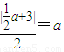 ,解得a=2,
,解得a=2,
∴c=1,b=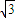 ,
,
所求椭圆方程为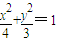
点评:本题主要考查了直线与圆锥曲线的综合问题.解题的前提的是熟练掌握椭圆的基本性质.
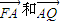 ,根据
,根据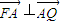 得出
得出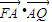 =0看,进而求得x,设P(x1,y1)根据
=0看,进而求得x,设P(x1,y1)根据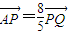 求得x1和y1的表达式,把点P的坐标代入椭圆方程进而求得a和c的关系,则椭圆的离心率可得.
求得x1和y1的表达式,把点P的坐标代入椭圆方程进而求得a和c的关系,则椭圆的离心率可得.(2)根据(1)中a和c的关系可知F和Q的坐标,△AQF的外接圆圆心和半径,进而根据
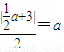 求得a,进而根据a和b,c的关系求得b,则椭圆的方程可得.
求得a,进而根据a和b,c的关系求得b,则椭圆的方程可得.解答:解:(1)设Q(x,0),由F(-c,0)A(0,b)知
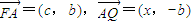
∵
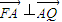 ,∴
,∴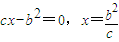
设P(x1,y1),
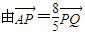 得
得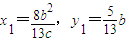
因为点P在椭圆上,所以
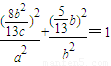
整理得2b2=3ac,即2(a2-c2)=3ac,2e2+3e-2=0,故椭圆的离心率e=
 .
.(2)由(1)知
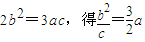 ,
,
于是F(-
 a,0)Q
a,0)Q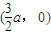 ,
,△AQF的外接圆圆心为(
 a,0),半径r=
a,0),半径r= |FQ|=a
|FQ|=a所以
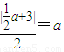 ,解得a=2,
,解得a=2,∴c=1,b=
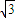 ,
,所求椭圆方程为
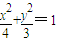
点评:本题主要考查了直线与圆锥曲线的综合问题.解题的前提的是熟练掌握椭圆的基本性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +
+ =1(a>b>0)的左焦点为F1=(-
=1(a>b>0)的左焦点为F1=(- ,0),椭圆过点P(-
,0),椭圆过点P(- ,
, )
) =1(a>b>0)的左、右焦点分别为F1、F2,离心率为
=1(a>b>0)的左、右焦点分别为F1、F2,离心率为 ,左焦点F1到直线l:
,左焦点F1到直线l: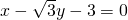 的距离等于长半轴长.
的距离等于长半轴长.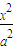 +
+ =1(a>b>0)过点M(1,1),离心率e=
=1(a>b>0)过点M(1,1),离心率e= ,O为坐标原点.
,O为坐标原点. •
• 为定值.
为定值. +
+ =1(a>b>0)的左焦点为F1=(-
=1(a>b>0)的左焦点为F1=(- ,0),椭圆过点P(-
,0),椭圆过点P(- ,
, )
)