题目内容
设集合 ,
, .
.
(1)当 1时,求集合
1时,求集合 ;
;
(2)当 时,求
时,求 的取值范围.
的取值范围.
(1)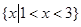 ;(2)
;(2)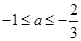 .
.
解析试题分析:(1)当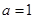 时,集合
时,集合 就是函数
就是函数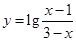 的定义域,解不等式
的定义域,解不等式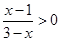 就可得到集合
就可得到集合 ;(2)由
;(2)由 知
知 ,集合
,集合 是不等式
是不等式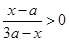 的解集,在解不等式时可先化为一元二次不等式,然后对相应方程的根的大小进行讨论,具体化集合
的解集,在解不等式时可先化为一元二次不等式,然后对相应方程的根的大小进行讨论,具体化集合 ,再由
,再由 确定
确定 的取值范围.
的取值范围.
试题解析: (1)当 1时,
1时,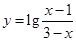 ,由
,由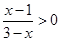 , 3分
, 3分
解得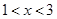 ,所以集合
,所以集合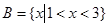 ; 7分
; 7分
(2)因为 ,则
,则 , 8分
, 8分
由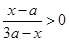 ,得
,得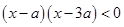 .
.
(ⅰ)当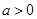 时,
时,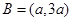 ,显然不满足题意; 10分
,显然不满足题意; 10分
(ⅱ)当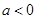 时,
时,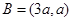 ,由题意知
,由题意知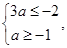 解得
解得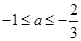 . 13分
. 13分
综上所述,所求 的取值范围是
的取值范围是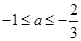 . 14分
. 14分
考点:集合的运算、子集的含义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设全集 ,集合
,集合 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知集合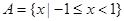 ,
,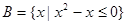 ,则
,则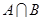 等于( )
等于( )
A.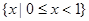 | B.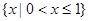 |
C.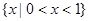 | D.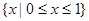 |
 是整数集
是整数集 的非空子集,如果
的非空子集,如果 有
有 ,则称
,则称 关于数的乘法是封闭的. 若
关于数的乘法是封闭的. 若 ,
, 是
是 且
且 有
有 有
有 ,有四个命题:①
,有四个命题:① 中至少有一个关于乘法是封闭的;②
中至少有一个关于乘法是封闭的;② 用列举法表示为 .
用列举法表示为 . 为全集,
为全集, .
. 时,求
时,求 及
及 ;
; ,求实数
,求实数 的取值范围.
的取值范围. ,集合
,集合

 时,求
时,求 ;
; ,求实数
,求实数 的取值范围.
的取值范围. ,
, ,
, ,求
,求 ;
; ,求实数a的取值范围.
,求实数a的取值范围.