题目内容
设x>0,y>0,且x+4y=40,则lgx+lgy的最大值是( )
| A.40 | B.10 | C.4 | D.2 |
D
∵x+4y=40,且x>0,y>0,
∴x+4y≥2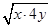 =4
=4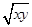 .(当且仅当x=4y时取“=”)
.(当且仅当x=4y时取“=”)
∴4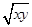 ≤40.
≤40.
∴xy≤100.
∴lgx+lgy=lg(xy)≤lg100=2.
∴lgx+lgy的最大值为2.
∴x+4y≥2
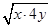 =4
=4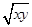 .(当且仅当x=4y时取“=”)
.(当且仅当x=4y时取“=”)∴4
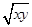 ≤40.
≤40.∴xy≤100.
∴lgx+lgy=lg(xy)≤lg100=2.
∴lgx+lgy的最大值为2.

练习册系列答案
相关题目
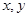 满足
满足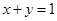 ,求
,求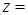
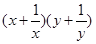 的最小值.
的最小值.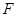 (单位时间内测量点的车辆数,单位:辆/小时)与车流速度
(单位时间内测量点的车辆数,单位:辆/小时)与车流速度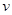 (假设车辆以相同速度
(假设车辆以相同速度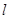 (单位:米)的值有关,其公式为
(单位:米)的值有关,其公式为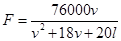
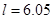 ,则最大车流量为_______辆/小时;
,则最大车流量为_______辆/小时;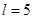 ,则最大车流量比(1)中的最大车流量增加 辆/小时.
,则最大车流量比(1)中的最大车流量增加 辆/小时.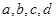 满足:
满足: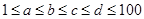 ,则
,则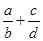 取得最小值时,
取得最小值时,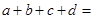
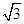 是
是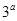 和
和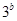 的等比中项,则
的等比中项,则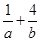 的最小值为( )
的最小值为( )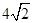
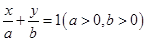 过点
过点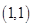 ,则
,则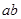 的最小值为_________.
的最小值为_________.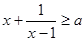 恒成立,则实数
恒成立,则实数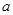 的取值范围是
的取值范围是