题目内容
【题目】已知I为△ABC的内心,cosA= ![]() ,若
,若 ![]() =x
=x ![]() +y
+y ![]() ,则x+y的最大值为( )
,则x+y的最大值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:设圆I与△ABC三边的切点为D、E、F,则cos∠BAC=2cos2∠DAI﹣1= ![]() ,∴cos∠DAI=
,∴cos∠DAI= ![]() ,
,
设圆I的半径为1,则AD=AE= ![]() ,AI=4,
,AI=4,
设BD=BF=m,CF=CE=n,
由余弦定理得cos∠BAC= ![]() =
= ![]() ,
,
整理可得:mn= ![]() +1≤(
+1≤( ![]() )2.
)2.
∴m+n≥ ![]() .
.
∵I为△ABC的内心,
∴(m+n) ![]() +(n+
+(n+ ![]() )
) ![]() +(m+
+(m+ ![]() )
) ![]() =
= ![]() ,
,
∴(m+n) ![]() +(n+
+(n+ ![]() )(
)( ![]() )+(m+
)+(m+ ![]() )(
)( ![]() +
+ ![]() )=
)= ![]() ,
,
∴ ![]() =
= ![]() +
+ ![]() ,
,
∴x+y= ![]() =
= ![]() +
+ ![]() ≤
≤ ![]() +
+ ![]() =
= ![]() .
.
所以答案是:D.
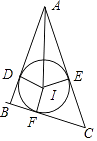
【考点精析】解答此题的关键在于理解平面向量的基本定理及其意义的相关知识,掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.

练习册系列答案
相关题目