题目内容
我们把由半椭圆
+
=1(x≥0)与半椭圆
+
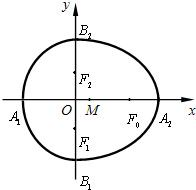
=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角,则a,b的值分别为( )

| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| c2 |
A.
| B.
| C.5,3 | D.5,4 |

OF2=
=
,OF0=c=
OF2=
,∴b=1,
∴a2=b2+c2=1+
=
,得a=
,即a=
,b=1.
故选A
| b2-c2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴a2=b2+c2=1+
| 3 |
| 4 |
| 7 |
| 4 |
| ||
| 2 |
| ||
| 2 |
故选A

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 我们把由半椭圆
我们把由半椭圆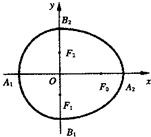 我们把由半椭圆
我们把由半椭圆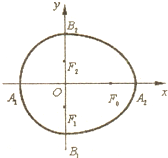 请阅读以下材料,然后解决问题:
请阅读以下材料,然后解决问题: