题目内容
设集合A= ,x,y∈R},B={(x,y)|4x+ay-16=0,x,y∈R}若A∩B=Φ,则a的值为( )
,x,y∈R},B={(x,y)|4x+ay-16=0,x,y∈R}若A∩B=Φ,则a的值为( )A.4
B.-2
C.4或-2
D.2或-4
【答案】分析:由题意知集合A,B为点集,集合A= ,y∈R},B={(x,y)|4x+ay-16=0,x,y∈R},分别解出集合A,B,根据A∩B=Φ,说明两直线无交点,从而求出a的范围.
,y∈R},B={(x,y)|4x+ay-16=0,x,y∈R},分别解出集合A,B,根据A∩B=Φ,说明两直线无交点,从而求出a的范围.
解答:解:∵集合A=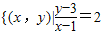 ,y∈R},
,y∈R},
∴A={(x,y)|y=2x+1,x≠1},∴点(1,3)不在直线y=2x+1上,
∵B={(x,y)|4x+ay-16=0,x,y∈R},
又∵A∩B=Φ,
∴直线y=2x+1与直线4x+ay-16=0,没有交点,或者点点(1,3)在4x+ay-16=0上也满足,
∴2=-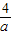 或4×1+a×3-16=0,
或4×1+a×3-16=0,
解得a=-2或4,
故选C.
点评:此题主要考查的是点组成集合,概念不清会导致部分同学失分,另外注意x≠1这个条件,说明点(1,3)不在直线y=2x+1上,
从而解得a=4,很多同学都漏掉这个答案.
 ,y∈R},B={(x,y)|4x+ay-16=0,x,y∈R},分别解出集合A,B,根据A∩B=Φ,说明两直线无交点,从而求出a的范围.
,y∈R},B={(x,y)|4x+ay-16=0,x,y∈R},分别解出集合A,B,根据A∩B=Φ,说明两直线无交点,从而求出a的范围.解答:解:∵集合A=
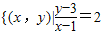 ,y∈R},
,y∈R},∴A={(x,y)|y=2x+1,x≠1},∴点(1,3)不在直线y=2x+1上,
∵B={(x,y)|4x+ay-16=0,x,y∈R},
又∵A∩B=Φ,
∴直线y=2x+1与直线4x+ay-16=0,没有交点,或者点点(1,3)在4x+ay-16=0上也满足,
∴2=-
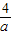 或4×1+a×3-16=0,
或4×1+a×3-16=0,解得a=-2或4,
故选C.
点评:此题主要考查的是点组成集合,概念不清会导致部分同学失分,另外注意x≠1这个条件,说明点(1,3)不在直线y=2x+1上,
从而解得a=4,很多同学都漏掉这个答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目