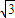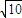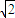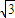Question

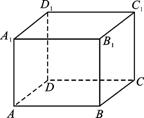
长方体AC₁的长、宽、高分别为3、2、1，从A到C₁沿长方体的表面的最短距离为（    ）

A.1+                B.2+                C.3                D.2

   

Answer 1

活动:解决空间几何体表面上两点间最短线路问题，一般都是将空间几何体表面展开，转化为求平面内两点间线段长，这体现了数学中的转化思想.

解：如图3，在长方体ABCD—A₁B₁C₁D₁中，AB=3，BC=2，BB₁=1.

图3

如图4所示，将侧面ABB₁A₁和侧面BCC₁B₁展开,

图4

则有AC₁==，即经过侧面ABB₁A₁和侧面BCC₁B₁时的最短距离是；

如图5所示，将侧面ABB₁A₁和底面A₁B₁C₁D₁展开,

则有AC₁==3，即经过侧面ABB₁A₁和底面A₁B₁C₁D₁时的最短距离是3；

图5

如图6所示，将侧面ADD₁A₁和底面A₁B₁C₁D₁展开,

图6

则有AC₁==2，即经过侧面ADD₁A₁和底面A₁B₁C₁D₁时的最短距离是2.

由于3＜2，3＜，所以由A到C₁在正方体表面上的最短距离为3.

答案：C

点评：本题主要考查空间几何体的简单运算及转化思想.求表面上最短距离可把图形展成平面图形.