题目内容
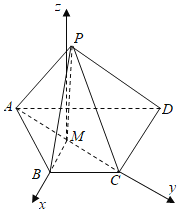
【题目】如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,![]() ,
,![]()
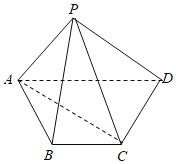
(Ⅰ)证明;AC⊥BP;
(Ⅱ)求直线AD与平面APC所成角的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】
(I)取![]() 的中点
的中点![]() ,连接
,连接![]() ,通过证明
,通过证明![]() 平面
平面![]() 得出
得出![]() ;
;
(II)以![]() 为原点建立坐标系,求出平面
为原点建立坐标系,求出平面![]() 的法向量
的法向量![]() ,通过计算
,通过计算![]() 与
与![]() 的夹角得出
的夹角得出![]() 与平面
与平面![]() 所成角.
所成角.
(I)证明:取AC的中点M,连接PM,BM,
∵AB=BC,PA=PC,
∴AC⊥BM,AC⊥PM,又BM∩PM=M,
∴AC⊥平面PBM,
∵BP平面PBM,
∴AC⊥BP.
(II)解:∵底面ABCD是梯形.BC∥AD,AB=BC=CD=1,AD=2,
∴∠ABC=120°,
∵AB=BC=1,∴AC![]() ,BM
,BM![]() ,∴AC⊥CD,
,∴AC⊥CD,
又AC⊥BM,∴BM∥CD.
∵PA=PC![]() ,CM
,CM![]() ,∴PM
,∴PM![]() ,
,
∵PB![]() ,∴cos∠BMP
,∴cos∠BMP![]() ,∴∠PMB=120°,
,∴∠PMB=120°,
以M为原点,以MB,MC的方向为x轴,y轴的正方向,
以平面ABCD在M处的垂线为z轴建立坐标系
则A(0,![]() ,0),C(0,
,0),C(0,![]() ,0),P(
,0),P(![]() ,0,
,0,![]() ),D(﹣1,
),D(﹣1,![]() ,0),
,0),
∴![]() (﹣1,
(﹣1,![]() ,0),
,0),![]() (0,
(0,![]() ,0),
,0),![]() (
(![]() ,
,![]() ,
,![]() ),
),
设平面ACP的法向量为![]() (x,y,z),则
(x,y,z),则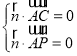 ,即
,即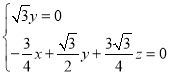 ,
,
令x![]() 得
得![]() (
(![]() ,0,1),
,0,1),
∴cos![]() ,
,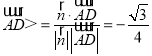 ,
,
∴直线AD与平面APC所成角的正弦值为|cos![]() ,
,![]() |
|![]() .
.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目